题目内容
11.函数f(x)=sin(x+$\frac{π}{3}$)+sin(x-$\frac{π}{3}$)的最大值是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
分析 利用两角和与差的三角函数化简函数的解析式,通过正弦函数求解最值.
解答 解:函数f(x)=sin(x+$\frac{π}{3}$)+sin(x-$\frac{π}{3}$)
=$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx+$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx
=sinx≤1.
故选:B.
点评 本题考查三角函数的最值的求法,考查计算能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 的值域是( )
的值域是( ) B.
B. C.
C. D.
D.
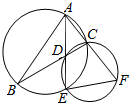 如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.
如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.