题目内容
1.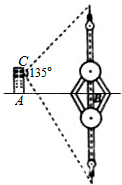 如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.
如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.
分析 过C作转播塔的垂线,设转播塔高度为h,用h表示出在C处对塔尖的仰角和对塔尖倒影的俯角的正切值,使用和角的正切函数列出方程解出h.
解答 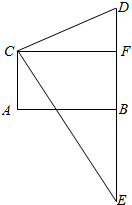 解:设转播塔尖为D,塔尖倒影为E,过C作CF⊥DE于F,则四边形ABFC是矩形,∴CF=AB=200,BF=AC=100,
解:设转播塔尖为D,塔尖倒影为E,过C作CF⊥DE于F,则四边形ABFC是矩形,∴CF=AB=200,BF=AC=100,
设传播塔高为h,则DF=h-100,EF=h+100,
∴tan∠DCF=$\frac{h-100}{200}$,tan∠ECF=$\frac{h+100}{200}$,
∵∠DCF+∠ECF=135°,
∴tan135°=$\frac{\frac{h-100}{200}+\frac{h+100}{200}}{1-\frac{h-100}{200}×\frac{h+100}{200}}$=-1.解得h=500.
∴转播塔的高度为500米.
点评 本题考查了解三角形的应用,和角的正切公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知f(x)=-x2+10,则f(x)在x=$\frac{3}{2}$处的瞬时变化率是( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |

 ,应用秦九韶算法计算
,应用秦九韶算法计算 时的值时,
时的值时, =_____
=_____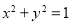 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线 .
.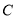 的参数方程;
的参数方程;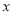 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线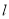 的极坐标方程为
的极坐标方程为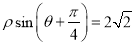 ,若
,若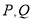 分别为曲线
分别为曲线 和直线
和直线 上的一点,求
上的一点,求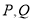 的最近距离.
的最近距离.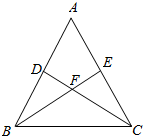 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.