题目内容
4.函数y=x2-(4a+1)x+3a2+3a的图象与x轴交于A、B两点,若两点间的距离等于2,则a的值为( )| A. | $\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$或-$\frac{1}{2}$ | D. | $\frac{3}{2}$或-$\frac{2}{3}$ |
分析 利用根与系数的关系列方程解出a.
解答 解:∵函数与x轴有两个交点,∴△>0.
即(4a+1)2-12a2-12a=4a2-4a+1=(2a-1)2>0,
∴a$≠\frac{1}{2}$.
设A,B的横坐标分别为x1,x2,
则x1+x2=4a+1,x1x2=3a2+3a,
∴|AB|=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=|2a-1|=2,
解得a=$\frac{3}{2}$或a=-$\frac{1}{2}$.
故选C.
点评 本题考查了二次函数的性质,根与系数的关系,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
12.抛掷一枚均匀的硬币4次,则恰有2次正面向上的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
16.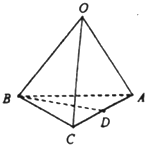 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )| A. | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
13.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的渐近线方程为( )
| A. | 4x±9y=0 | B. | 9x±4y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |