题目内容
17.已知复数z满足z=$\frac{1+2i}{2-i}$,则|z|=1.分析 利用复数代数形式的乘除运算化简,然后代入复数模的计算公式求解.
解答 解:∵z=$\frac{1+2i}{2-i}$=$\frac{(1+2i)(2+i)}{(2-i)(2+i)}=\frac{5i}{5}=i$,
∴|z|=1.
故答案为:1.
点评 本题考查复数代数形式的乘除运算,考查复数模的求法,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.抛掷一枚均匀的硬币4次,则恰有2次正面向上的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
6.在复平面内,复数z=-2+i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
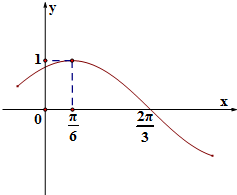 已知函数f(x)=Asin(ωx+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$,ω>0,A>0)其部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$,ω>0,A>0)其部分图象如图所示: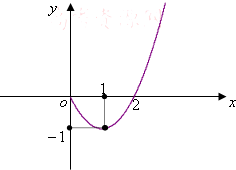 已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).
已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).