题目内容
12．若tanθ=2，则$\frac{2sinθ-cosθ}{sinθ+2cosθ}$的值为（ ）| A． | 0 | B． | 1 | C． | $\frac{3}{4}$ | D． | $\frac{5}{4}$ |
分析 将所求分子分母同除cosθ，利用同角三角函数基本关系式化简，代入tanθ=2，即可得到选项．
解答 解：∵tanθ=2，
∴$\frac{2sinθ-cosθ}{sinθ+2cosθ}$=$\frac{2tanθ-1}{tanθ+2}$=$\frac{2×2-1}{2+2}$=$\frac{3}{4}$．
故选：C．
点评 本题是基础题，考查同角三角函数基本关系式的应用，已知函数值求表达式的其它函数值，考查计算能力，常考题型．
练习册系列答案
相关题目
2．若函数f（x）是定义在R上的偶函数，在（-∞，0）上对任意两个不相等的实数a，b总有$\frac{f（a）-f（b）}{a-b}$＞0，且f（2）=0，则使xf（x）＜0的x的取值范围是（ ）
| A． | -2＜x＜2 | B． | x＞2或-2＜x＜0 | C． | -2＜x＜0 | D． | x＜-2或x＞2 |
7．命题：“对任意 x＞0，ex＞x+1”的否定是（ ）
| A． | 存在 x≤0，ex≤x+1 | B． | 存在 x＞0，ex≤x+1 | ||
| C． | 存在 x≤0，ex＞x+1 | D． | 对任意 x＞0，ex≤x+1 |
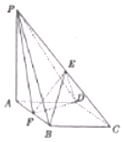如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=3，PA⊥底面ABCD，E，F分别是PC，AB的中点．