题目内容
14.在平面直角坐标系xoy中,双曲线$\frac{x^2}{{2{m^2}}}-\frac{y^2}{3m}=1$的焦距为6,则所有满足条件的实数m构成的集合是{$\frac{3}{2}$}.分析 根据题意,先由双曲线的方程分析可得m的取值范围,进而又由该双曲线的焦距为6,则有c=3,即$\sqrt{2{m}^{2}+3m}$=3,解可得m的值,结合m的范围可得m的值,用集合表示即可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{x^2}{{2{m^2}}}-\frac{y^2}{3m}=1$,则有$\left\{\begin{array}{l}{2{m}^{2}>0}\\{3m>0}\end{array}\right.$,解可得m>0,
则有c=$\sqrt{2{m}^{2}+3m}$,
又由该双曲线的焦距为6,则有c=3,
即$\sqrt{2{m}^{2}+3m}$=3,
解可得:m=-3或$\frac{3}{2}$,
又由m>0,
则m=$\frac{3}{2}$;
即所有满足条件的实数m构成的集合是{$\frac{3}{2}$};
故答案为:{$\frac{3}{2}$}.
点评 本题考查双曲线的几何性质,注意焦距是2c.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
5.在区域$Ω=\left\{{(x,y)|\left\{\begin{array}{l}x≥0\\ x+y≤1\\ x-y≤1\end{array}\right.}\right\}$中,若满足ax+y>0的区域面积占Ω面积的$\frac{1}{3}$,则实数a的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{2}{3}$ |
9.甲盒子中有编号分别为1,2的两个乒乓球,乙盒子中有编号分别为3,4,5,6的四个乒乓球.现分别从两个盒子中随机地各取出1个乒乓球,则取出的乒乓球的编号之和大于6的概率为$\frac{3}{8}$.
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
| A. | $\frac{2}{3}$钱 | B. | $\frac{5}{6}$钱 | C. | 1钱 | D. | $\frac{7}{6}$钱 |
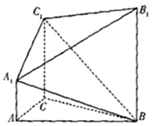 如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.
如图,在几何体A1B1C1-ABC中,∠ACB=90°,AC=BC=2,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1,且AA1=1.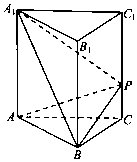
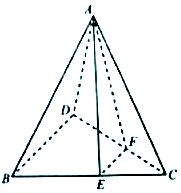 如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.
如图,在三棱锥A-BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.