题目内容
5．函数$f（x）=\frac{1}{3}{x^3}+a{x^2}+x+1$有极大值和极小值，则实数a取值范围是（-∞，-1）∪（1，+∞）．分析 先求导函数，根据函数f（x）既有极大值又有极小值，可得f′（x）=0有两个不等的实数根，从而可求实数a的取值范围．
解答 解：求导函数可得，f′（x）=x2+2ax+1，
∵函数f（x）既有极大值又有极小值，
∴f′（x）=x2+2ax+1=0有两个不等的实数根，
∴△=4a2-4＞0，
∴a＞1或a＜-1，
故答案为：（-∞，-1）∪（1，+∞）．
点评 本题考查导数知识的运用，考查函数的极值，考查解不等式，属于基础题．
练习册系列答案
相关题目
15．已知双曲线的中心在原点，两个焦点F1，F2分别为$（-\sqrt{5}，0）和（\sqrt{5}，0）$，点P在双曲线上，PF1⊥PF2，且△PF1F2的面积为1，则双曲线的方程为（ ）
| A． | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | B． | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | C． | $\frac{x^2}{4}-{y^2}=1$ | D． | ${x^2}-\frac{y^2}{4}=1$ |
16．已知Sn是公比为q的等比数列{an}的前n项和．若3S1，2S2，S3成等差数列，则q=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 3 |
13．设x，y∈N*，x+y=10，xy＞20的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{5}{9}$ | C． | $\frac{2}{3}$ | D． | $\frac{7}{9}$ |
20．已知命题p：“?x∈R，x2-2x+2＞0”，则￢p是（ ）
| A． | ?x∈R，x2-2x+2≤0 | B． | ?x0∈R，$x_0^2-2{x_0}+2＞0$ | ||
| C． | ?x0∈R，$x_0^2-2{x_0}+2＜0$ | D． | ?x0∈R，$x_0^2-2{x_0}+2≤0$ |
14．一个正三棱柱的三视图如图所示，则这个正三棱柱的侧面积为（ ）
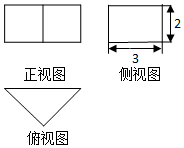
| A． | 18 | B． | $18\sqrt{3}$ | C． | $6\sqrt{3}$ | D． | $12\sqrt{3}$ |
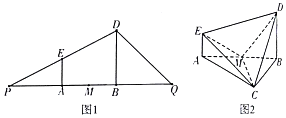已知△PDQ中，A，B分别为边PQ上的两个三等分点，BD为底边PQ上的高，AE∥DB，如图1，将△PDQ分别沿AE，DB折起，使得P，Q重合于点C．AB中点为M，如图2．