题目内容
15.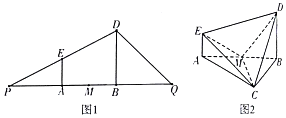 已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.
已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.(Ⅰ)求证:CM⊥EM;
(Ⅱ)若直线DM与平面ABC所成角的正切值为2,求二面角B-CD-E的大小.
分析 (Ⅰ)推导出△ABC是等边三角形,从而CM⊥AB,再由DB⊥AB,DB⊥BC,知DB⊥平面ABC,又EA∥DB,从而EA⊥平面ABC,进而CM⊥EA.由此CM⊥平面EAM.进而能证明CM⊥EM.
(Ⅱ)以点M为坐标原点,MC所在直线为x轴,MB所在直线为y轴,过M且与直线BD平行的直线为z轴,建立空间直角坐标系M-xyz.利用向量法能求出二面角B-CD-E的平面角.
解答 证明:(Ⅰ)因为A,B是PQ的三等分点,
所以PA=AB=BQ=CA=CB,
所以△ABC是等边三角形,又因为M是AB的中点,所以CM⊥AB.
因为DB⊥AB,DB⊥BC,AB∩BC=B,
所以DB⊥平面ABC,又EA∥DB,
所以EA⊥平面ABC,
CM?平面ABC,所以CM⊥EA.
因为AM∩EA=A,所以CM⊥平面EAM.
因为EA?平面EAM,所以CM⊥EM.
解:(Ⅱ)以点M为坐标原点,MC所在直线为x轴,MB所在直线为y轴,
过M且与直线BD平行的直线为z轴,建立空间直角坐标系M-xyz.
因为DB⊥平面ABC,
所以∠DMB为直线DM与平面ABC所成角.
由题意得tan$∠DMB=\frac{BD}{MB}=2$,即BD=2MB,
从而BD=AC.不防设AC=2,又AC+2AE,则CM=$\sqrt{3}$,AE=1.
故B(0,1,0),C($\sqrt{3}$,0,0),D(0,1,2),E(0,-1,1).
于是$\overrightarrow{BC}$=($\sqrt{3}$,-1,0),$\overrightarrow{BD}$=(0,0,2),$\overrightarrow{CE}$=(-$\sqrt{3},-1,1$),$\overrightarrow{CD}$=(-$\sqrt{3}$,1,2),
设平面BCD与平面CDE的法向量分别为$\overrightarrow{m}$=(x,y,z),$\overrightarrow{n}$=(a,b,c),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=3x-y=0}\\{\overrightarrow{m}•\overrightarrow{BD}=2z=0}\end{array}\right.$,令x=1,得$\overrightarrow{m}$=(1,$\sqrt{3}$,0).
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CE}=-\sqrt{3}a-b+c=0}\\{\overrightarrow{n}•\overrightarrow{CD}=-\sqrt{3}a+b+2c=0}\end{array}\right.$,令a=1,得$\overrightarrow{n}$=(1,-$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),
所以cos<$\overrightarrow{m},\overrightarrow{n}$>=0.
所以二面角B-CD-E的平面角大小为90°.
点评 本题考查线线垂直的证明,考查二面角的求法,考查推理论证能力、运算求解能力,考查等价转化思想、数形结合思想,考查空间思维能力,是中档题.

 口算题天天练系列答案
口算题天天练系列答案| A. | $\frac{1}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{31}{32}$ | D. | $\frac{23}{32}$ |
| A. | 可以小于0 | B. | 只能大于0 | C. | 可以为0 | D. | 只能小于0 |
| A. | {-1} | B. | {1,2} | C. | {0,3} | D. | {-1,1,2,3} |
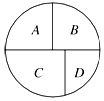 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.| A. | 120种 | B. | 150 种 | C. | 180 种 | D. | 240 种 |