题目内容
点F为椭圆
+
=1(a>b>0)的一个焦点,若椭圆上存在点A使△AOF为正三角形,那么椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,写出焦点F的坐标,然后,根据△AOF为正三角形,建立等式,求解其离心率.
解答:
解:如下图所示:

设椭圆的右焦点为F,根据椭圆的对称性,得
直线OF的斜率为k=tan60°=
,
∴点P坐标为:(
c,
c),
代人椭圆的标准方程,得
+
=1,
∴b2c2+3a2c2=4a2b2,
∴e=
-1.
故选:D.

设椭圆的右焦点为F,根据椭圆的对称性,得
直线OF的斜率为k=tan60°=
| 3 |
∴点P坐标为:(
| 1 |
| 2 |
| ||
| 2 |
代人椭圆的标准方程,得
| ||
| a2 |
| ||
| b2 |
∴b2c2+3a2c2=4a2b2,
∴e=
| 3 |
故选:D.
点评:本题重点考查了椭圆的概念和基本性质,属于中档题.求解离心率的解题关键是想法设法建立关于a,b,c的等量关系,然后,进行求解.

练习册系列答案
相关题目
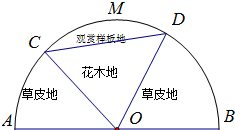 某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
 某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为
某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为