题目内容
将一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设两条直线l1:ax+by=2,l2:x+2y=2,l1与l2平行的概率为P1,相交的概率为P2,则P2-P1的大小为 .
考点:几何概型
专题:
分析:本题是两个古典概型的问题,试验发生包含的事件是一颗骰子投掷两次,共有36种结果,使得两条直线平行的a,b的值可以通过列举做出,还有一种就是使得两条直线重合,除此之外剩下的是相交的情况,写出概率做出差.
解答:
解:由题意知本题是两个古典概型的问题,
试验发生包含的事件是一颗骰子投掷两次,第一次出现的点数记为a,
第二次出现的点数记为b,共有36种结果,
要使的两条直线?1:ax+by=2,?2:x+2y=2平行,
则a=2,b=4;a=3;b=6,共有2种结果,
当A=1,B=2时,两条直线平行,
其他33种结果,都使的两条直线相交,
∴两条直线平行的概率是
,
两条直线相交的概率是
,
∴两个概率之差是
,
故答案为:
.
试验发生包含的事件是一颗骰子投掷两次,第一次出现的点数记为a,
第二次出现的点数记为b,共有36种结果,
要使的两条直线?1:ax+by=2,?2:x+2y=2平行,
则a=2,b=4;a=3;b=6,共有2种结果,
当A=1,B=2时,两条直线平行,
其他33种结果,都使的两条直线相交,
∴两条直线平行的概率是
| 2 |
| 36 |
两条直线相交的概率是
| 33 |
| 36 |
∴两个概率之差是
| 31 |
| 36 |
故答案为:
| 31 |
| 36 |
点评:本题考查古典概型问题,考查两条直线的平行,相交和重合的充要条件,是一个综合题目,也是一个易错题,注意容易漏掉重合的情况.

练习册系列答案
相关题目
双曲线C:
-
=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),M是双曲线上的一点,且满足
•
+2a2=0,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| F2M |
A、(1,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
点F为椭圆
+
=1(a>b>0)的一个焦点,若椭圆上存在点A使△AOF为正三角形,那么椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
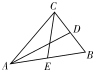 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E分别是BC、AB的中点,P是△ABC(包括边界)内任一点,则
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E分别是BC、AB的中点,P是△ABC(包括边界)内任一点,则| AD |
| EP |
| A、[-7,7] |
| B、[-8,8] |
| C、[-9,9] |
| D、[-10,O] |
 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BBC,AP的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BBC,AP的中点.