题目内容
若
•
+
2=0，则△ABC为（ ）
| AB |
| BC |
| AB |
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等边三角形 |
考点：三角形的形状判断
专题：解三角形
分析：由条件根据两个向量的加减法的法则，以及其几何意义，两个向量垂直的条件可得
⊥
，从而得出结论．
| AB |
| AC |
解答：
解：△ABC中，∵
•
+
2=0，∴
•（
+
）=0，即
•
=0，故有
⊥
，
∴∠A=
，∴△ABC为直角三角形，
故选：A．
| AB |
| BC |
| AB |
| AB |
| AB |
| BC |
| AB |
| AC |
| AB |
| AC |
∴∠A=
| π |
| 2 |
故选：A．
点评：本题主要考查两个向量垂直的条件，两个向量的加减法的法则，以及其几何意义，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
《张丘建算经》卷上第22题为：今有女善织，日益功疾，且从第2天起，每天比前一天多织相同量的布，若第1天织5尺布，现在一月（按30天计）共织390尺布，则每天比前一天多织（ ）尺布．（不作近似计算）
A、
| ||
B、
| ||
C、
| ||
D、
|
若sin2θ-1+（
+1）i是纯虚数，则θ的值为（ ）
| 2 |
A、2kπ-
| ||||
B、kπ+
| ||||
C、2kπ±
| ||||
D、
|
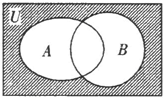设全集U={1，2，3，4，5，6，7，8}，集合A={2，4，5，7}，B={1，4，7，8}，那么如图所示的阴影部分所表示的集合是（ ）| A、{3，6} |
| B、{4，7} |
| C、{1，2，4，5，7，8} |
| D、{1，2，3，5，6，8} |
三个实数a，b，c依次成公差不为零的等差数列，且a，c，b成等比数列，则
的值是（ ）
| a |
| b |
| A、-2 | B、2 | C、4 | D、-4 |
根据如图给出的数塔猜测123456×9+7=（ ）
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |