题目内容
在△ABC中,若
=
,
=
(1)若D为BC上的点,且
=t
,求证:
=(1-t)
+t
;
(2)若P,Q是线段BC的三等分点,试证:
+
=
+
;
(3)若P,Q,S是线段BC的四等分点,试证:
+
+
=
(
+
)
(4)如果A1,A2,A3,…An-1是线段BC的n(n≥3)等分点,你能得到什么结论?并加以证明.(注:1+2+3+…+n=
)
| AB |
| a |
| AC |
| b‘ |
(1)若D为BC上的点,且
| BD |
| BC |
| AD |
| a |
| b |
(2)若P,Q是线段BC的三等分点,试证:
| AP |
| AQ |
| a |
| b |
(3)若P,Q,S是线段BC的四等分点,试证:
| AP |
| AQ |
| AS |
| 3 |
| 2 |
| a |
| b |
(4)如果A1,A2,A3,…An-1是线段BC的n(n≥3)等分点,你能得到什么结论?并加以证明.(注:1+2+3+…+n=
| n(n+1) |
| 2 |
考点:线段的定比分点,平面向量的基本定理及其意义
专题:平面向量及应用
分析:(1)画出图形,结合图形,根据向量的加减法运算法则,得出
的向量表示;
(2)当P,Q是线段BC的三等分点时,利用平行四边形法则,得出
+
=
+
=
+
;
(3)当P,Q,S是线段BC的四等分点时,根据向量的合成法则,得出
+
=
+
=2
,从而得出结论;
(4)当A1,A2,A3,…An-1是线段BC的n(n≥3)等分点时,得出
+
+
+…+
=
(
+
);
结合图形,利用向量的加减运算,证明即可.
| AD |
(2)当P,Q是线段BC的三等分点时,利用平行四边形法则,得出
| AP |
| AQ |
| AB |
| AC |
| a |
| b |
(3)当P,Q,S是线段BC的四等分点时,根据向量的合成法则,得出
| AB |
| AC |
| AP |
| AS |
| AQ |
(4)当A1,A2,A3,…An-1是线段BC的n(n≥3)等分点时,得出
| AA1 |
| AA2 |
| AA3 |
| AAn-1 |
| n-1 |
| 2 |
| a |
| b |
结合图形,利用向量的加减运算,证明即可.
解答:
解:(1)△ABC中,
=
,
=
,D为BC上的点,且
=t
,
如图1所示:
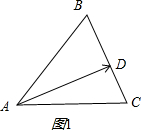
∴
=
+
=
+t
=
+t(
-
)=(1-t)
+t
=(1-t)
+t
;
(2)当P,Q是线段BC的三等分点时,以AB、AC为邻边作平行四边形ABDC,连接AD,交BC于O点,
连接PD,QD,如图2所示:
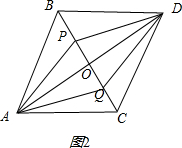
则
+
=
,
∵OB=OC,BP=CQ=
BC,
∴OP=OQ,且OA=OD,
∴四边形ABDC是平行四边形,
∴
+
=
=
+
=
+
;
(3)当P,Q,S是线段BC的四等分点时,如图3所示:
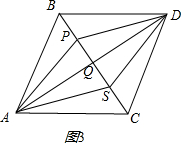
则Q是BC的中点,
+
=
+
=2
∴
+
+
=
(
+
)=
(
+
)
(4)当A1,A2,A3,…An-1是线段BC的n(n≥3)等分点时,
+
+
+…+
=
(
+
);如图所示:
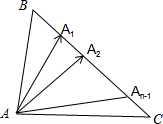 :
:
证明如下,∵
=
-
=
-
=
-
,
=
-
=
-
,…,
同理
=
-
,
∴
+
+…+
=(n-1)
-(
+
+..+
)
=(n-1)
-
•
=(n-1)
-
(
-
)
=
(
+
)
=
(
+
).
| AB |
| a |
| AC |
| b‘ |
| BD |
| BC |
如图1所示:

∴
| AD |
| AB |
| BD |
| AB |
| BC |
| AB |
| AC |
| AB |
| AB |
| AC |
| a |
| b |
(2)当P,Q是线段BC的三等分点时,以AB、AC为邻边作平行四边形ABDC,连接AD,交BC于O点,
连接PD,QD,如图2所示:

则
| AB |
| AC |
| AD |
∵OB=OC,BP=CQ=
| 1 |
| 3 |
∴OP=OQ,且OA=OD,
∴四边形ABDC是平行四边形,
∴
| AP |
| AQ |
| AD |
| AB |
| AC |
| a |
| b |
(3)当P,Q,S是线段BC的四等分点时,如图3所示:

则Q是BC的中点,
| AB |
| AC |
| AP |
| AS |
| AQ |
∴
| AP |
| AQ |
| AS |
| 3 |
| 2 |
| AB |
| AC |
| 3 |
| 2 |
| a |
| b |
(4)当A1,A2,A3,…An-1是线段BC的n(n≥3)等分点时,
| AA1 |
| AA2 |
| AA3 |
| AAn-1 |
| n-1 |
| 2 |
| a |
| b |
 :
:证明如下,∵
| AA1 |
| BA1 |
| BA |
| AB |
| A1B |
| AB |
| 1 |
| n |
| CB |
| AA2 |
| AB |
| A2B |
| AB |
| 2 |
| n |
| CB |
同理
| AAn-1 |
| AB |
| n-1 |
| n |
| CB |
∴
| AA1 |
| AA2 |
| AAn-1 |
| AB |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| CB |
=(n-1)
| AB |
| n(n-1) |
| 2 |
| 1 |
| n |
| CB |
=(n-1)
| AB |
| n-1 |
| 2 |
| AB |
| AC |
=
| n-1 |
| 2 |
| AB |
| AC |
=
| n-1 |
| 2 |
| a |
| b |
点评:本题考查了平面向量的加减运算的几何意义,也考查了类比推理的应用问题,是综合性题目.

练习册系列答案
相关题目
幂函数f(x)=xα的图象经过点(2,4),则f(9)=( )
| A、1 | B、3 | C、9 | D、81 |
下列双曲线中,渐近线方程是y=±
x的是( )
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC的三条边长分别为8,10,15,则该三角形为( )
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、不能确定 |
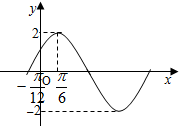 已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<