题目内容
已知数列{an}中,a1=1,且对任意的正整数m、n满足am+n=am+an+2mn,求a2014.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:令m=1,得到a1+n=a1+an+2n=an+2n+1,利用累加法即可得到结论.
解答:
解:∵a1=1,且对任意的正整数m、n满足am+n=am+an+2mn,
∴令m=1,得到an+1=a1+an+2n=an+2n+1,
即an+1-an=2n+1,
则a2-a1=3,
a3-a2=5,
a4-a3=7,
…
a2014-a2013=2×2013+1=4027,
两边同时相加,
则a2014-a1=3+5+…+4027,
即a2014=1+3+5+…+4027=
×2014=2014×2014=20142
∴令m=1,得到an+1=a1+an+2n=an+2n+1,
即an+1-an=2n+1,
则a2-a1=3,
a3-a2=5,
a4-a3=7,
…
a2014-a2013=2×2013+1=4027,
两边同时相加,
则a2014-a1=3+5+…+4027,
即a2014=1+3+5+…+4027=
| 1+4027 |
| 2 |
点评:本题主要考查数列递推公式的应用,利m=1,利用累加法是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
圆C:(x-1)2+(y+2)2=5的圆心坐标和半径分别为( )
| A、(1,2),5 | ||
| B、(1,-2),5 | ||
C、(1,-2),
| ||
D、(-1,2),
|
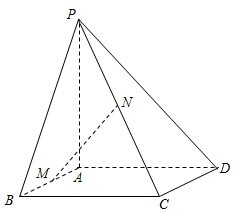 如图,在四棱锥中,底面ABCD为矩形,PA⊥底面ABCD,M、N分别是AB、PC中点.
如图,在四棱锥中,底面ABCD为矩形,PA⊥底面ABCD,M、N分别是AB、PC中点.