题目内容
已知tanθ+
=2，则sinθ+cosθ等于（ ）
| 1 |
| tanθ |
| A、2 | ||
B、
| ||
C、-
| ||
D、±
|
考点：同角三角函数基本关系的运用,三角函数的化简求值
专题：计算题,三角函数的求值
分析：先求出tanθ，再求出sinθ=cosθ=±
，即可得出结论．
| ||
| 2 |
解答：
解：∵tanθ+
=2，
∴tanθ=1，
∴sinθ=cosθ=±
，
∴sinθ+cosθ=±
．
故选：D．
| 1 |
| tanθ |
∴tanθ=1，
∴sinθ=cosθ=±
| ||
| 2 |
∴sinθ+cosθ=±
| 2 |
故选：D．
点评：本题考查同角三角函数基本关系的运用，比较基础．
练习册系列答案
全能测控期末小状元系列答案
相关题目
函数f（x）=
x3-4x+4的极大值与极小值之和为（ ）
| 1 |
| 3 |
| A、8 | ||
B、
| ||
| C、10 | ||
| D、12 |
已知直线l1：3x-
y+1=0与直线l2：
x-3y+2=0，则l1与l2的夹角为（ ）
| 3 |
| 3 |
| A、150° | B、120° |
| C、60° | D、30° |
已知复数z满足z（1-i）=（1+i）2，其中i为虚数单位，则复数z的共轭复数为（ ）
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
如果a＜b＜0，那么下面一定成立的是（ ）
A、
| ||||
| B、ac＜bc | ||||
| C、a-b＞0 | ||||
| D、a2＜b2 |
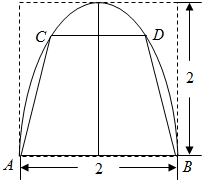如图，有一块抛物线形状的钢板，计划将此钢板切割成等腰梯形ABCD的形状，使得A，B，C，D都落在抛物线上，点A，B关于抛物线的轴对称，且AB=2，抛物线的顶点到底边的距离是2，记CD=2t，梯形面积为S．