Question

2．已知函数f（x）=|2x-1|+|2x+a|，g（x）=x+3．
（Ⅰ）当a=-2时，求不等式f（x）＜g（x）的解集；
（Ⅱ）设a＞-1，且当x∈[-$\frac{a}{2}$，$\frac{1}{2}$]时，f（x）≤g（x），求a的取值范围．

Answer 1

分析 （Ⅰ）当a=-2时，求不等式f（x）＜g（x）化为|2x-1|+|2x-2|-x-3＜0．设y=|2x-1|+|2x-2|-x-3，画出函数y的图象，数形结合可得结论．
（Ⅱ）不等式化即 1+a≤x+3，故x≥a-2对x∈[-$\frac{a}{2}$，$\frac{1}{2}$]都成立，分析可得-$\frac{a}{2}$≥a-2，由此解得a的取值范围．

解答 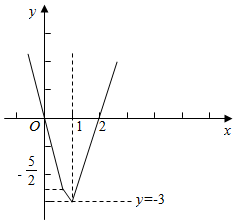解：（Ⅰ）当a=-2时，求不等式f（x）＜g（x）化为|2x-1|+|2x-2|-x-3＜0．
设y=|2x-1|+|2x-2|-x-3，则 y=$\left\{\begin{array}{l}{-5x\\，x＜\frac{1}{2}}\\{-x-2\\，\frac{1}{2}≤x≤1}\\{3x-6\\，x＞1}\end{array}\right.$，它的图象如图所示：
结合图象可得，y＜0的解集为（0，2），故原不等式的解集为（0，2）．
（Ⅱ）设a＞-1，且当x∈[-$\frac{a}{2}$，$\frac{1}{2}$]时，f（x）=1+a，不等式化为 1+a≤x+3，
故 x≥a-2对x∈[-$\frac{a}{2}$，$\frac{1}{2}$]都成立．
故-$\frac{a}{2}$≥a-2，
解得 a≤$\frac{4}{3}$，
故a的取值范围为（-1，$\frac{4}{3}$]．

点评 本题考查绝对值不等式的解法与绝对值不等式的性质，关键是利用零点分段讨论法分析函数的解析式．