题目内容
若复数z=（m2-7m+15）+（m2-5m+3）i（m∈R，i为虚数单位）在复平面内对应的点位于直线y=-x上，则m= ．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：由题意得到复数z的实部和虚部互为相反数，由此列式求解m的值．
解答：
解：∵复数z=（m2-7m+15）+（m2-5m+3）i在复平面内对应的点位于直线y=-x上，
∴m2-5m+3=-m2+7m-15，
即（m-3）2=0．
解得：m=3．
故答案为：3．
∴m2-5m+3=-m2+7m-15，
即（m-3）2=0．
解得：m=3．
故答案为：3．
点评：本题考查了复数的代数表示法及其几何意义，是基础的计算题．
练习册系列答案
名校课堂系列答案
相关题目
在长为8的线段AB上任取一点C，现作一矩形，邻边长分别等于AC、BC的长，则该矩形面积大于15的概率（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
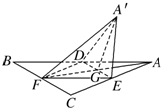如图，正三角形ABC的中线AF与中位线DE相交于点G，已知△A′ED是△AED绕DE旋转过程中的一个图形，现给出下列四个命题：
数字1，2，3，…，9这九个数字填写在如图的9个空格中，要求每一行从左到右依次增大，每列从上到下也依次增大，当数字4固定在中心位置时，则所有填写空格的方法共有如图给出的是计算1+
+
+…+
的值的一个程序框图，其中判断框内应填入的条件是（ ）
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 11 |
| A、i＜12 | B、i＞11 |
| C、i＜11 | D、i≤6 |