题目内容

12．若f（x）=$\left\{{\begin{array}{l}{{a^x}，x＜0}\\{{{log}_a}x，x＞0}\end{array}}$，那么y=f（x）-a的零点个数有（　　）
A．0个B．1个
C．2个D．a的值不同时零点的个数不同

分析 分别画出a＞1和0＜a＜1时的图象，判断两个函数的图象交点个数即可．

解答 解：画出a＞1时，f（x）=$\left\{{\begin{array}{l}{{a^x}，x＜0}\\{{{log}_a}x，x＞0}\end{array}}$，
与y=a的图象如图：
两个函数的图象只有一个交点．
当0＜a＜1时，f（x）=$\left\{{\begin{array}{l}{{a^x}，x＜0}\\{{{log}_a}x，x＞0}\end{array}}$，与y=a的图象如下图：
两个函数的图象只有一个交点，可知无论a为何值，均有1个零点．
故选：B．

点评 本题考查函数的零点与方程根的关系，考查数形结合以及计算能力．

练习册系列答案
相关题目
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上一点P（1，$\frac{3}{2}$）与椭圆右焦点的连线垂直于x轴，直线l：y=kx+m与椭圆C相交于A、B两点（均不在坐标轴上）．
（1）求椭圆C的标准方程；
（2）设O为坐标原点，若△AOB的面积为$\sqrt{3}$，试判断直线OA与OB的斜率之积是否为定值？若是，求出该定值；若不是，说明理由．
3．已知方程2x2+3x-1=0的一非零实根是x1，ax2+3x-1=0（a≠0）的一非零实根是x2．函数f（x）=$\frac{1}{3}{x^3}+\frac{3}{2}{x^2}$-x+3在（x1，x2）有且仅有一个极值点，则a的取值范围是[-$\frac{9}{4}$，0）∪（0，1]．
20．已知函数f（x）=$\left\{\begin{array}{l}{-{2}^{x}+2，x≤1}\\{\frac{1}{2}x-\frac{1}{2}，x＞1}\end{array}\right.$，若存在实数x1＜x2，使得f（x1）=f（x2），则x2f（x1）的取值范围是（0，10）．
7．抛物线y2=2px的焦点为F，过点F斜率为k的直线交抛物线于A，B两点，以AB为直径的圆与直线k：x=-2相切，则p的值为（　　）
A．2B．4C．6D．由k的值确定
17．一个正三棱柱的主（正）视图是长为2$\sqrt{3}$，宽为4的矩形，则它的外接球的表面积等于（　　）
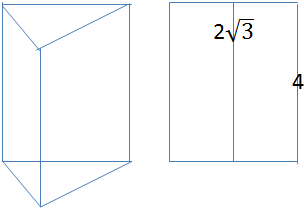
A．64πB．48πC．32πD．16π
4．已知曲线C：ρ=$\frac{2}{1-sinθ}$，直线l：$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$ （t为参数，0≤α＜π）．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）设直线l与曲线C交于A、B两点（A在第一象限），当$\overrightarrow{OA}$+3$\overrightarrow{OB}$=$\overrightarrow{0}$时，求α的值．
1．命题p：若“?x0∈[0，$\frac{π}{4}$]，tanx0＞m-3”是假命题，则实数m的最小值为4．
4．在向南方雪灾受灾地区的捐款活动中，某慈善组织收到一笔10000元的匿名捐款，该组织经过调查，发现是甲、乙、丙、丁四个人当中的某一个捐的．慈善组织成员对他们进行求证时，发现他们的说法互相矛盾．
甲说：对不起，这钱不是我捐的
乙说：我估计这钱肯定是丁捐的
丙说：乙的收入最高，肯定是乙捐的
丁说：乙的说法没有任何根据
假定四人中只有一个说了真话，那么真正的捐款者是甲（仅一人）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网