题目内容
4.在向南方雪灾受灾地区的捐款活动中,某慈善组织收到一笔10000元的匿名捐款,该组织经过调查,发现是甲、乙、丙、丁四个人当中的某一个捐的.慈善组织成员对他们进行求证时,发现他们的说法互相矛盾.甲说:对不起,这钱不是我捐的
乙说:我估计这钱肯定是丁捐的
丙说:乙的收入最高,肯定是乙捐的
丁说:乙的说法没有任何根据
假定四人中只有一个说了真话,那么真正的捐款者是甲(仅一人).
分析 由已知中四人中只有一个说了真话,而且乙和丙说法对立,可得甲丙说的一定是假话,即钱是甲捐的.
解答 解:∵四人中只有一个说了真话,而且乙和丙说法对立,
故甲丙说的一定是假话,
即钱是甲捐的,
此时乙说的是假话,丁说的是真话,满足条件;
故答案是:甲
点评 本题考查的知识点是合情推理,简单逻辑,正确理解乙和丙说法对立,是解答的关键.

练习册系列答案
相关题目
12.若f(x)=$\left\{{\begin{array}{l}{{a^x},x<0}\\{{{log}_a}x,x>0}\end{array}}$,那么y=f(x)-a的零点个数有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | a的值不同时零点的个数不同 |
12.随机变量X的分布列如下:若E(X)=$\frac{15}{8}$,则D(X)等于( )
| X | 1 | 2 | 3 |
| P | 0.5 | x | y |
| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{33}{64}$ | D. | $\frac{55}{64}$ |
19.直线l过点P(-1,2),且倾斜角为45°,则直线l的方程为( )
| A. | x-y+1=0 | B. | x-y-1=0 | C. | x-y-3=0 | D. | x-y+3=0 |
9.已知函数f(x)=$\left\{{\begin{array}{l}{(2-a)x+3a,x<1}\\{{{log}_2}x,x≥1}\end{array}}\right.$的值域为R,则实数a的取值范围是( )
| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1] | D. | {-1} |
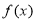 和
和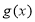 分别是
分别是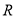 上的偶函数和奇函数,则下列结论恒成立的是( )
上的偶函数和奇函数,则下列结论恒成立的是( )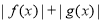 是偶函数 B.
是偶函数 B.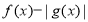 是奇函数
是奇函数 是偶函数 D.
是偶函数 D.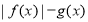 是奇函数
是奇函数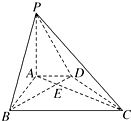 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.