题目内容
9.已知函数f(x)=$\left\{{\begin{array}{l}{(2-a)x+3a,x<1}\\{{{log}_2}x,x≥1}\end{array}}\right.$的值域为R,则实数a的取值范围是( )| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1] | D. | {-1} |
分析 根据分段函数的值域为R,具有连续性,由y=log2x是增函数,可得y=(2-a)x+3a也是增函数,故得2-a>0,(2-a)+3a≤0,可得答案.
解答 解:函数f(x)=$\left\{{\begin{array}{l}{(2-a)x+3a,x<1}\\{{{log}_2}x,x≥1}\end{array}}\right.$的值域为R,
由y=log2x是增函数,
∴y=(2-a)x+3a也是增函数,
故得2-a>0,
解得:a<2,
∵函数f(x)的值域为R,
(2-a)×1+3a≥log21,
解得:a≥-1.
∴实数a的取值范围是[-1,2).
故选B.
点评 本题考察了分段函数的性质的运用能力和计算能力.属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
17.一个正三棱柱的主(正)视图是长为2$\sqrt{3}$,宽为4的矩形,则它的外接球的表面积等于( )
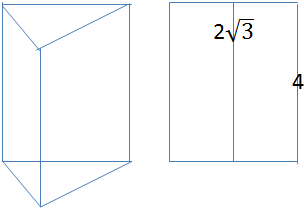

| A. | 64π | B. | 48π | C. | 32π | D. | 16π |
17.已知正方体ABCD-A1B1C1D1棱长为1,E、F为线段B1D1的两个动点,且EF=$\frac{\sqrt{2}}{2}$,给出下列四个命题:
①AC⊥BE;
②EF∥平面ABCD;
③点B到平面AEF的距离为定值;
④异面直线AE与BF所成的角为定值.
其中真命题的个数为( )
①AC⊥BE;
②EF∥平面ABCD;
③点B到平面AEF的距离为定值;
④异面直线AE与BF所成的角为定值.
其中真命题的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个. |
14.曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{25-k}$=1(0<k<9)的关系是( )
| A. | 有相等的焦距,相同的焦点 | B. | 有不同的焦距,不同的焦点 | ||
| C. | 有相等的焦距,不同的焦点 | D. | 以上都不对 |
 ,集合
,集合 ,则( )
,则( ) B.
B.
 D.
D.