题目内容
14.曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{25-k}$=1(0<k<9)的关系是( )| A. | 有相等的焦距,相同的焦点 | B. | 有不同的焦距,不同的焦点 | ||
| C. | 有相等的焦距,不同的焦点 | D. | 以上都不对 |
分析 判断两个椭圆的焦点坐标与焦距的大小即可得到结果.
解答 解:曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{25-k}$=1(0<k<9)都是椭圆方程,焦距为:2c=$\sqrt{25-9}$=8,$\sqrt{25-k-(9-k)}$=8,焦距相等,$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦点坐标在x轴,$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{25-k}$=1的焦点坐标在y轴,
故选:C.
点评 本题考查椭圆的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
5.已知等比数列{an}中,a1+a2+a3+a4+a5=31,a2+a3+a4+a5+a6=62,则通项an等于( )
| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
9.已知函数f(x)=$\left\{{\begin{array}{l}{(2-a)x+3a,x<1}\\{{{log}_2}x,x≥1}\end{array}}\right.$的值域为R,则实数a的取值范围是( )
| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1] | D. | {-1} |
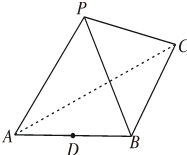 在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.
在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.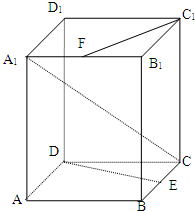 已知棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,F为A1B1的中点.
已知棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,F为A1B1的中点. 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.