题目内容
16.已知数列{an}是等比数列,a3=4,且a3是a2+4与a4+14的等差中项;数列{bn}是等差数列,b2=16,其前n项和Tn满足Tn=nλ•bn+1(λ为常数,且λ≠1).(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式及λ的值.
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用等差数列及其前n项和公式即可得出.
解答 解:(1)设等比数列{an}的公比为q.
∵a3是a2+4与a4+14的等差中项.
∴2a3=a2+4+a4+14,又a3=4,
∴8=$\frac{4}{q}$+4+4q+14,
化为2q2+5q+2=0,
解得q=-2或q=-$\frac{1}{2}$.
当q=-2时,数列{an}的通项公式为an=${a}_{3}{q}^{n-3}$=4×(-2)n-3=(-2)n-1.
当q=-$\frac{1}{2}$时,数列{an}的通项公式为an=${a}_{3}{q}^{n-3}$=$4×(-\frac{1}{2})^{n-3}$=$(-\frac{1}{2})^{n-5}$.
(2)设数列{bn}的公差为d.
由Tn=nλ•bn+1,
得$\left\{\begin{array}{l}{{T}_{1}=λ{b}_{2}}\\{{T}_{2}=2λ{b}_{3}}\end{array}\right.$,
得$\left\{\begin{array}{l}{16-d=16λ}\\{16-d+16=2λ(16+d)}\end{array}\right.$,解得$\left\{\begin{array}{l}{d=0}\\{λ=1}\end{array}\right.$(舍去),或$\left\{\begin{array}{l}{d=8}\\{λ=\frac{1}{2}}\end{array}\right.$.
此时数列{bn}的通项公式为bn=b2+(n-2)d=16+8(n-2)=8n,
则bn+1=8(n+1),b1=8,
数列{bn}的前n项和为Tn=8n+$\frac{n(n-1)}{2}$×8=4n(n+1),
而nλ•bn+1=n×$\frac{1}{2}$8(n+1)=4n(n+1),满足Tn=nλbn+1,符合题意,
∴数列{bn}的通项公式为bn=8n且$λ=\frac{1}{2}$.
点评 本题考查了等比数列与等差数列的通项公式及其前n项和公式、递推关系的应用,考查了推理能力与计算能力,属于中档题.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案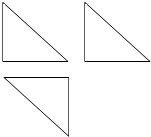 如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
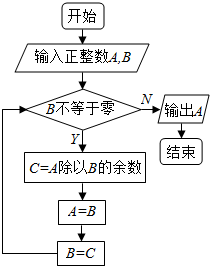
| A. | 90 | B. | 45 | C. | 2 | D. | 0 |
| A. | x=$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相同 | B. | x=-$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相同 | ||
| C. | x=$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相反 | D. | x=-$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相反 |
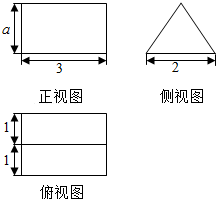 如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.