题目内容
设a,b为非零向量,则以下说法不正确的是( )
A、“
| ||||||||||||
B、“
| ||||||||||||
C、“|
| ||||||||||||
D、“|
|
考点:平面向量数量积的运算
专题:阅读型,平面向量及应用
分析:运用向量共线和垂直的条件,以及向量共线定理,结合充分必要条件的定义,即可判断正误.
解答:
解:对于A.由两向量共线的概念,可知
=
⇒
∥
,反之不成立,
则“
=
”是“
∥
”的充分不必要条件,则A正确;
对于B.
=
⇒
∥
,反之不成立,
故“
=
”是“
∥
”的充分不必要条件,则B错误;
对于C.|
+
|=|
|-|
|⇒
,
共线,即存在λ∈R使得
=λ
,反之不成立,则C正确;
对于D.|
+
|=|
|-|
|⇒
∥
,但不能得到
⊥
,反之也不成立,则D正确.
故选B.
| a |
| b |
| a |
| b |
则“
| a |
| b |
| a |
| b |
对于B.
| AB |
| CD |
| AB |
| CD |
故“
| AB |
| CD |
| AB |
| CD |
对于C.|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
对于D.|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选B.
点评:本题考查向量的共线和垂直的条件,考查充分必要条件的判断,考查推理能力,属于基础题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设θ是第三象限的角,则点P(cosθ,tanθ)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
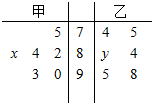 如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则x,y的值为( )
如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则x,y的值为( )| A、2,4 | B、4,4 |
| C、5,6 | D、6,4 |
两直线2x+3y-k=0和x+ky-12=0的交点在y轴上,那么k的值是( )
| A、-24 | B、6 | C、±6 | D、24 |
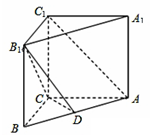 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.