题目内容
7.实数x,y满足x2=2xsin(xy)-1,则x2014+4sin13y=5.分析 由(x-sin(xy))2+cos2(xy)=0,知x=sin(xy),且cos(xy)=0,所以x=sin(xy)=±1.由此能求出x2014+6sin13y.
解答 解:∵x2=2xsin(xy)-1,
∴(x-sin(xy))2+cos2(xy)=0,
∴x=sin(xy)且cos(xy)=0,
∴x=sin(xy)=±1,
∴siny=1,x=1,
x2014+4sin13y=5,
故答案为:5.
点评 本题考查函数的值的求法,解题时要认真审题,仔细解答,注意三角函数性质的灵活运用.

练习册系列答案
相关题目
17.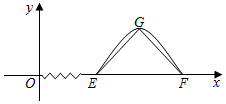 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是以G为顶点,EF为底边且长为4的等腰直角三角形,则f(100)=( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
2.若A={x|x=4k+1,k∈Z},B={x|x=2k-1,k∈Z},则( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |