题目内容
13. 某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;
某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;(2)现准备从分数在110-115的n名学生(女生占$\frac{1}{3}$)中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
(3)为了分析某个学生的学习状态,对其下一阶段的学习提供指导建议,对他前7次考试的数学成绩x、物理成绩y进行分析,该生7次考试成绩如表
| 数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘估计分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i-}\overline{x})^{2}}$,$\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$.
分析 (1)根据题意,计算分数在100-110内的频率,求出该班总人数,再计算分数在110-115内的频率,计算对应的人数;
(2)求出分数6名学生中女生有2名,得出6名学生中选出3人,女生人数ξ的可能取值,再计算对应的概率值,写出ξ的分布列,计算数学期望值;
(3)计算$\overline{x}$、$\overline{y}$,求出回归系数$\stackrel{∧}{b}$、写出对应线性回归方程,根据方程计算x=130时$\stackrel{∧}{y}$的值即可.
解答 解:(1)分数在100-110内的学生的频率为P1=(0.04+0.03)×5=0.35,
所以该班总人数为N=$\frac{21}{0.35}$=60,
分数在110-115内的学生的频率为
P2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1,
分数在110-115内的人数为n=60×0.1=6;
(2)由题意分数在110-115内有6名学生,其中女生有2名,
从6名学生中选出3人,女生人数ξ的可能取值为0,1,2;
则P(ξ=0)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,P(ξ=1)=$\frac{{C}_{2}^{1}{•C}_{4}^{2}}{{C}_{6}^{3}}$=$\frac{3}{5}$,P(ξ=2)=$\frac{{C}_{2}^{2}{•C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$;
所以ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
(3)计算$\overline{x}$=$\frac{1}{7}$×(88+83+117+92+108+100+112)=100,
$\overline{y}$=$\frac{1}{7}$×(94+91+108+96+104+101+106)=100;
由于x与y之间具有线性相关关系,
根据回归系数公式得到$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i-}\overline{x})^{2}}$=$\frac{497}{994}$=0.5,
$\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$=100-0.5×100=50,
∴线性回归方程为$\stackrel{∧}{y}$=0.5x+50,
∴当x=130时,$\stackrel{∧}{y}$=0.5×130+50=115.
点评 本题考查了频率分布直方图与线性回归方程以及分布列和数学期望的计算问题,是综合性题目.

练习册系列答案
相关题目
1.2016年1月1日起全国统一实施全面的两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后80后作为调查对象,随机调查了100人并对调查结果进行统计,70后不打算生二胎的占全部调查人数的15%,80后打算生二胎的占全部被调查人数的45%,100人中共有75人打算生二胎.
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
(${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.某个路口交通指示灯,红灯时间为30秒,黄灯时间为10秒,绿灯时间为40秒,黄灯时间可以通行,当你到达路口时,等待时间不超过10秒就可以通行的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
13.高二某班共有学生60人,座号分别为1,2,3,…,60现根据座号,用系统抽样的方法,抽取一个容量为5的样本.已知4号、28号、40号、52号同学在样本中,那么样本中还有一个同学的座号是( )
| A. | 14 | B. | 16 | C. | 36 | D. | 56 |
14.已知函数f(x)=$\frac{\sqrt{5-ax}}{a-2}$(a∈A),若f(x)在区间(0,1]上是减函数,则集合A可以是( )
| A. | (-∞,0) | B. | [1,2) | C. | (-1,5] | D. | [4,6] |
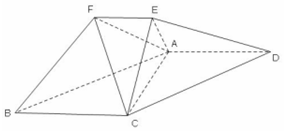 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,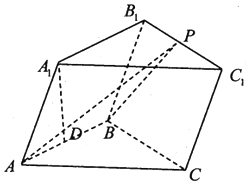 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.