题目内容
17．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F2（c，0）作圆x2+y2=a2的切线，切点为M，延长F2M交抛物线y2=-4cx于点P，其中O为坐标原点，若$\overrightarrow{OM}=\frac{1}{2}（\overrightarrow{O{F_2}}+\overrightarrow{OP}）$，则双曲线的离心率为（ ）| A． | $\frac{4\sqrt{2}-2}{7}$ | B． | $\frac{4\sqrt{2}+2}{7}$ | C． | $\frac{1+\sqrt{3}}{2}$ | D． | $\frac{1+\sqrt{5}}{2}$ |
分析 说明M是F2P的中点．设抛物线的焦点为F1，则F1为（-c，0），也是双曲线的焦点．画出图形，连接PF1，OM，说明OM为△PF2F1的中位线．通过PF2⊥PF1，可得|PF2|=$\sqrt{4{c}^{2}-4{a}^{2}}=2b$，设P（x，y），推出 c-x=2a，利用双曲线定义结合勾股定理得 y2+4a2=4b2，然后求解离心率即可．
解答 
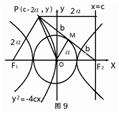解：如图9，∵$\overrightarrow{OM}=\frac{1}{2}（\overrightarrow{O{F_2}}+\overrightarrow{OP}）$，∴M是F2P的中点．
设抛物线的焦点为F1，则F1为（-c，0），也是双曲线的焦点．
连接PF1，OM．∵O、M分别是F1F2和PF2的中点，∴OM为
△PF2F1的中位线．∵OM=a，∴|PF1|=2 a．∵OM⊥PF2，
∴PF2⊥PF1，于是可得|PF2|=$\sqrt{4{c}^{2}-4{a}^{2}}=2b$，设P（x，y），则 c-x=2a，
于是有x=c-2a，y2=-4c（c-2 a），过点F2作x轴的垂线，点P到该垂线的距离为2a．
由勾股定理得 y2+4a2=4b2，即-4c（c-2a）+4 a2=4（c2-a2），
变形可得c2-a2=ac，两边同除以a2
有 e2-e-1=0，所以e=$\frac{1+\sqrt{5}}{2}$，负值已经舍去．
故选：D．
点评 本题考查双曲线的简单性质的应用，向量以及圆与双曲线的位置关系的综合应用，考查转化思想以及计算能力．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
12．过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F1作x轴的垂线交椭圆于P、Q两点，F2为右焦点，若△PQF2为等边三角形，则椭圆的离心率为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
2．在△ABC中，设D是AB边上的一点，且$\overrightarrow{AD}$=2$\overrightarrow{DB}$，则（ ）
| A． | $\overrightarrow{CD}$=$\frac{1}{3}$$\overrightarrow{CA}$-$\frac{2}{3}$$\overrightarrow{CB}$ | B． | $\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{CA}$-$\frac{1}{3}$$\overrightarrow{CB}$ | C． | $\overrightarrow{CD}$=$\frac{1}{3}$$\overrightarrow{CA}$+$\frac{2}{3}$$\overrightarrow{CB}$ | D． | $\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{CB}$ |