题目内容

13．已知0＜a＜1，分别在区间（0，a）和（0，4-a）内任取一个数，且取出的两数之和小于1的概率为$\frac{3}{16}$．则a的值为$\frac{4}{5}$．

分析 分类讨论，分别计算其面积，由几何概型的计算公式可得答案．

解答 解：由题意，$\frac{\frac{1}{2}}{a（4-a）}$=$\frac{3}{16}$，∴a=$\frac{6±2\sqrt{3}}{3}$，不合题意；
$\frac{\frac{1}{2}（1-a+1）a}{a（4-a）}$=$\frac{3}{16}$，∴a=$\frac{4}{5}$．
故答案为：$\frac{4}{5}$．

点评 本题考查几何概型的计算，解题的关键在于用平面区域表示出题干的代数关系．

练习册系列答案
相关题目
3．定义在[-1，1]上的奇函数f（x）有最小正周期2，当0＜x＜1时，f（x）=$\frac{2^x}{{{4^x}+1}}$．
（1）讨论f（x）在（0，1）上的单调性；
（2）求f（x）在[-1，1]的表达式；
（3）函数y=f（x）-a有零点，求实数a的取值范围．
4．奇函数f（x）当x∈（0，+∞）时的解析式为f（x）=x2-x+2，则f（-1）=（　　）
A．-2B．2C．4D．-4
1．有一个容量为100的样本，数据的分组及各组的频数如下：
[12，14），6；[14，16），16；[16，18），18；[18，20），22； 
[20，22），20；[22，24），10；[24，26），8；
（1）列出样本的频率分布表；
（2）画出频率分布直方图和频率折线图．
8．若全集U={1，2，3，4}且∁UA={1}，则集合A的真子集共有（　　）
A．3个B．5个C．7个D．8个
18．求函数f（x）的解析式．
（1）已知f（x）是一次函数，且满足3f（x+1）-2f（x）=2x+17
（2）已知f（$\frac{x+1}{x}$）=$\frac{{x}^{2}+x+1}{{x}^{2}}$，求f（x）．
5．已知$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是平面内两个不共线的向量，$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=-2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$，$\overrightarrow{c}$=7$\overrightarrow{{e}_{1}}$-4$\overrightarrow{{e}_{2}}$，试用$\overrightarrow{a}$、$\overrightarrow{b}$表示$\overrightarrow{c}$．
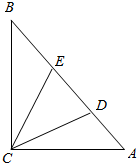2．如图，在Rt△ABC中，∠A=60°，AB=6，点D、E是斜边AB上两点．
（1）当点D是线段AB靠近A的一个三等分点时，求$\overrightarrow{CD}•\overrightarrow{CA}$的值；
（2）当点D、E在线段AB上运动时，且∠DCE=30°，设∠ACD=θ．试用θ表示△DCE的面积S，并求S的取值范围．
3．若${∫}_{\;}^{\;}$${\;}_{0}^{T}$x2dx=9，则常数T的值为（　　）
A．9B．-3C．3D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网