题目内容
8．若全集U={1，2，3，4}且∁UA={1}，则集合A的真子集共有（ ）| A． | 3个 | B． | 5个 | C． | 7个 | D． | 8个 |
分析 求出集合A，然后求解真子集的个数即可．
解答 解：全集U={1，2，3，4}且∁UA={1}，
可得A={2，3，4}．
集合A的真子集共有：23-1=7．
故选：C．
点评 本题主要考查集合的补集运算以及真子集个数的求法，只要利用公式即可得到答案，属易题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
18．若函数f（x）为偶函数，且在（0，∞）内是增函数，又f（-2015）=0，则不等式xf（x）＜0的解集是（ ）
| A． | {x|x＜-2015或0＜x＜2015} | B． | {x|x＜-2015＜x＜0或x＞2015} | ||
| C． | {x|x＜-2015或x＞2015} | D． | {x|-2015＜x＜0或0＜x＜2015} |
19．已知函数y=f（x）在R上为减函数，且f（0）=1，f（1）=0，则f（x）＞0的解集是（ ）
| A． | （0，+∞） | B． | （0，1） | C． | （1，+∞） | D． | （-∞，1） |
3．
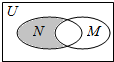设全集U=R，M={x|x＜-2，或x＞2}，N={x|1＜x＜3}，则图中阴影部分所表示的集合是（ ）
设全集U=R，M={x|x＜-2，或x＞2}，N={x|1＜x＜3}，则图中阴影部分所表示的集合是（ ）| A． | {x|-2≤x＜1} | B． | {x|-2≤x≤2} | C． | {x|1＜x≤2} | D． | {x|x＜2} |
20．已知集合M={x|x=$\frac{k}{5}+\frac{1}{10}$，k∈Z} N={x|$\frac{k}{10}+\frac{1}{5}$，k∈Z}，则（ ）
| A． | M=N | B． | M⊆N | C． | M?N | D． | M∩N=Φ |
18．二次函数y=2x2-2的图象为（ ）
| A． |  | B． |  | C． |  | D． |  |