题目内容
3.定义在[-1,1]上的奇函数f(x)有最小正周期2,当0<x<1时,f(x)=$\frac{2^x}{{{4^x}+1}}$.(1)讨论f(x)在(0,1)上的单调性;
(2)求f(x)在[-1,1]的表达式;
(3)函数y=f(x)-a有零点,求实数a的取值范围.
分析 (1)当0<x<1时,f(x)=$\frac{2^x}{{{4^x}+1}}$=$\frac{1}{{2}^{x}+\frac{1}{{2}^{x}}}$,利用y=${2}^{x}+\frac{1}{{2}^{x}}$在(1,2)上单调递增,即可得出f(x)在(0,1)上的单调性;
(2)利用奇函数的性质,求f(x)在[-1,1]的表达式;
(3)函数y=f(x)-a有零点,根据函数的值域,求实数a的取值范围.
解答 解:(1)当0<x<1时,f(x)=$\frac{2^x}{{{4^x}+1}}$=$\frac{1}{{2}^{x}+\frac{1}{{2}^{x}}}$,
∵y=${2}^{x}+\frac{1}{{2}^{x}}$在(1,2)上单调递增,
∴f(x)在(0,1)上的单调递减;
(2)$当-1<x<0时,f(x)=-f({-x})=-\frac{2^x}{{{4^x}+1}}$,
f(0)=0,f(-1)=-f(1),f(-1)=f(-1+2)=f(1),
∴f(-1)=f(1)=0,
∴$f(x)=\left\{\begin{array}{l}\frac{2^x}{{{4^x}+1}},0<x<1\\ 0,x=0或x=±1\\-\frac{2^x}{{{4^x}+1}},-1<x<0\end{array}\right.$
(3)$f(x)在({0,1})上递减,取值范围为({\frac{2}{5},\frac{1}{2}}),f(x)在({-1,0})上递减$,取值$范围为({-\frac{1}{2},-\frac{2}{5}})$,
f(0)=f(1)=f(-1)=0,$故a的范围为({\frac{2}{5},\frac{1}{2}})∪\left\{0\right\}∪({-\frac{1}{2},-\frac{2}{5}})$.
点评 本题考查奇偶性及函数单调性,考查函数解析式求解,综合性较强.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | {x|x<-2015或0<x<2015} | B. | {x|x<-2015<x<0或x>2015} | ||
| C. | {x|x<-2015或x>2015} | D. | {x|-2015<x<0或0<x<2015} |
| A. | f(-$\frac{3}{2}$)≥f(-a2-$\frac{3}{2}$) | B. | f(-$\frac{3}{2}$)<f(-a2-$\frac{3}{2}$) | C. | f(-$\frac{3}{2}$)>f(-a2-$\frac{3}{2}$) | D. | f(-$\frac{3}{2}$)≤f(-a2-$\frac{3}{2}$) |

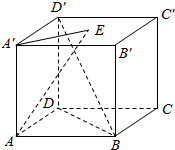 如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,取向量$\overrightarrow{AB}$、$\overrightarrow{AD}$、$\overrightarrow{AA′}$为基底的基向量,在下列条件下,分别求x、y、z的值
如图,已知正方体ABCD-A′B′C′D′,点E是上底面A′B′C′D′的中心,取向量$\overrightarrow{AB}$、$\overrightarrow{AD}$、$\overrightarrow{AA′}$为基底的基向量,在下列条件下,分别求x、y、z的值