题目内容
18.在区间[0,2π]上满足e0-eπ≤θ-sinθ-π的θ的取值范围是[0,2π].分析 由y=x-sinx(0≤x≤2π),求出导数,判断单调性可得0≤x-sinx≤2π,而e0-eπ+π<0,即可得到所求范围.
解答 解:e0-eπ≤θ-sinθ-π,
即为1+π-eπ≤θ-sinθ,
可令y=x-sinx(0≤x≤2π),
y′=1-cosx≥0,即函数y=x-sinx在[0,2π]递增,
可得0≤x-sinx≤2π,即0≤θ-sinθ≤2π,
而e0-eπ+π<0,
即有e0-eπ≤θ-sinθ-π在[0,2π]恒成立,
则θ的取值范围是[0,2π],
故答案为:[0,2π].
点评 本题考查不等式的解法,注意运用函数的单调性,结合不等式的性质,考查运算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )
| A. | (1,$\sqrt{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,3] |
3.函数f(x)=lg(3x-1)的定义域为( )
| A. | y=lnx | B. | (0,+∞) | C. | R | D. | ($\frac{1}{3}$,+∞) |
7.已知圆C:(x+m)2+y2=4上存在两点关于直线x-y+3=0对称,则实数m的值是( )
| A. | -3 | B. | 6 | C. | 3 | D. | 无法确定 |
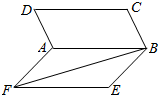 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.