题目内容
8.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )| A. | (1,$\sqrt{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,3] |
分析 由向量数量积的定义和性质,可得($\overrightarrow{a}$-$\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,再由基本不等式可得0<|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≤$\frac{1}{3}$,即可得到所求范围.
解答 解:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为120°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,
即有($\overrightarrow{a}$-$\overrightarrow{b}$)2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=$\overrightarrow{a}$2-2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°+$\overrightarrow{b}$2
=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≥2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|=3|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,
即有0<|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≤$\frac{1}{3}$,当且仅当|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,取得等号.
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2|\overrightarrow{a}|•|\overrightarrow{b}|cos120°}$=$\sqrt{1-2|\overrightarrow{a}|•|\overrightarrow{b}|}$,
即有$\frac{\sqrt{3}}{3}$≤|$\overrightarrow{a}$+$\overrightarrow{b}$|<1.
故选:B.
点评 本题考查向量的数量积的定义和性质,考查向量的平方即为模的平方,以及基本不等式的运用,考查运算能力,属于中档题.

| A. | f(-3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(-3) | C. | f(-2)<f(1)<f(-3) | D. | f(-3)<f(1)<f(-2) |
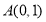 且斜率为
且斜率为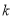 的直线
的直线 与圆
与圆 :
: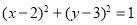 交于点
交于点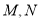 两点.
两点.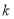 的取值范围;
的取值范围; ,其中
,其中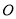 为坐标原点,求
为坐标原点,求 .
. 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直.  的值;
的值; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; .
.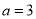 ,则输入的
,则输入的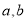 分别可能为( )
分别可能为( )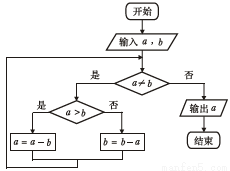
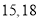 B.
B.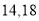 C.
C.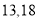 D.
D.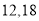
 如图,四棱锥C-ABED中,四边形ABED是正方形,若G,F分别是线段EC,BD的中点.
如图,四棱锥C-ABED中,四边形ABED是正方形,若G,F分别是线段EC,BD的中点.