题目内容

如图，已知P为△ABC内一点，且满足∠PAB=∠PBC=∠PCA=θ，求证：cotθ=cotA+cotB+cotC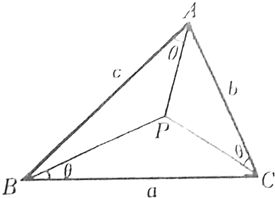
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：如图所示，设PA=x，PB=y，PC=z，利用余弦定理列出三个关系式，相加整理表示出cosθ，利用三角形面积公式列出关系式，整理表示出sinθ，进而利用同角三角函数间基本关系表示出cotθ，由余弦定理表示出cosA，利用三角形面积公式表示出sinA，进而表示出cotA，同理表示出cotB与cotC，代入cotA+cotB+cotC中，整理即可得证．
解答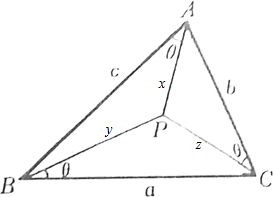： 证明：如图所示，设PA=x，PB=y，PC=z，
在△ABP中根据余弦定理有：2cxcosθ=x2+c2-y2①，
同理得到2aycosθ=y2+a2-z2②；2bzcosθ=z2+b2-x2③，
①+②+③得：2（cx+ay+bz）cosθ=a2+b2+c2，
整理得：cosθ=
a2+b2+c2
2(cx+ay+bz)
，
∵S△ABC=S△ABP+S△BCP+S△ACP=
1
2
cxsinθ+
1
2
aysinθ+
1
2
bzsinθ=
1
2
（cx+ay+bz）sinθ，
∴sinθ=
2S△ABC
cx+ay+bz
，
∴cotθ=
cosθ
sinθ
=
a2+b2+c2
4S△ABC
，
由余弦定理得：cosA=
b2+c2-a2
2bc
，根据面积公式得：sinA=
2S△ABC
bc
，
∴cotA=
cosA
sinA
=
b2+c2-a2
4S△ABC
，
同理可得cotB=
a2+c2-b2
4S△ABC
，cotC=
a2+b2-c2
4S△ABC
，
则cotA+cotB+cotC=
b2+c2-a2+a2+c2-b2+a2+b2-c2
4S△ABC
=
a2+b2+c2
4S△ABC
=cotθ．
点评：此题考查了同角三角函数间基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
在平面直角坐标系xOy中，已知点A（4，0），动点M在y轴上的正射影为点N，且满足直线MO⊥NA，则动点M的轨迹C的方程为
 
．
在区间[-1，2]上随机取一个数x，则|x|≤1的概率为（　　）
A、
2
3
B、
1
4
C、
1
3
D、
1
2
圆x2+y2-2x=0与圆x2+y2-4x-2y+1=0的位置关系为（　　）
A、相交B、相离C、外切D、内切
若圆O1：x2+y2=1与圆O2：（x-3）2+y2=r2（r＞0）相交，则r的范围为
 
．
等比数列{an}中，a4=2，a5=5，则数列{lgan}的前8项和等于（　　）
A、6B、5C、3D、4
集合A={-2＜x＜-1，或x＞0}，B={x|a≤x≤b}，且A∩B={x|0＜x≤2}，A∪B={x|x＞-2}，求a，b的值．
某产品的广告费用x（万元）与销售额y（万元）的统计数据如下表（一个数据上有污渍）：
广告费用x（万元）4235
销售额y（万元）492639
已知该公司根据原有统计数据（没有污渍前）得线性回归方程
y
=9.4x+9.1，则污渍部分的数据是（　　）
A、50B、52C、54D、58
在等腰直角△ABC中AC=BC，E为AC的中点，ED⊥AB于点D，将△ADE沿DE折起后为△A′DE使得面A′DE⊥面BCED．若F为线段A′B上一点及
A′F
A′B
=λ．
①当λ=
1
3
时，求证：FC∥面A′DE；
②当二面角∠B-DF-C的余弦值为值
3
7
，求λ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网