题目内容
复数满足在z（1-i）=2i，则复数Z的实部和虚部只差为（ ）
| A、-2 | B、2 | C、1 | D、0 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：把已知的等式变形，然后利用复数代数形式的乘除运算化简，求出实部和虚部，作差得答案．
解答：
解：∵z（1-i）=2i，
∴z=
=
=
=-1+i，
∴复数Z的实部和虚部分别为-1，1，差为-1-1=-2．
故选：A．
∴z=
| 2i |
| 1-i |
| 2i(1+i) |
| (1-i)(1+i) |
| -2+2i |
| 2 |
∴复数Z的实部和虚部分别为-1，1，差为-1-1=-2．
故选：A．
点评：本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
已知p：m-1＜x＜m+1，q：（x-2）（x-6）＜0，且q是p的必要不充分条件，则m的取值范围是（ ）
| A、3＜m＜5 |
| B、3≤m≤5 |
| C、m＞5或m＜3 |
| D、m≥5或m≤3 |
已知点p（-1，-
）在角θ的终边上，且θ∈[0，2π），则θ的值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
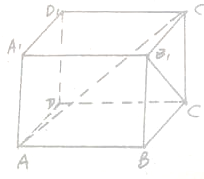已知长方体AC1中，AB=BC=4cm，AA1=2cm，E，F分别为BB1和A1B1的中点，求：