Question

11．某企业生产A、B两种产品，生产 1t产品所消耗的煤和电及所获利润如表：

产品	所需能源		利润（万元）
	煤（t）	电（kw•h）
A	6	6	9
B	4	9	1 2

又知两种产品的生产量不少于10t．该企业用电不超过360kw．h，用煤不超过240t，问生产A、B两种产品各多少吨时，才能获得最大的利润？最大的利润是多少？

Answer 1

分析 设出变量，列出不等式组，作出可行域，利用线性规划的知识即可得到结论．

解答 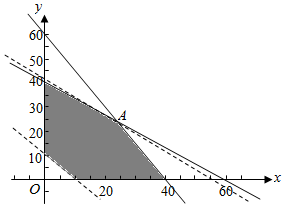解　设生产A，B两种产品各为x，y吨，利润为z万元，则
$\left\{\begin{array}{l}{6x+9y≤360}\\{6x+4y≤240}\\{x+y≥10}\\{x≥0，y≥0}\end{array}\right.$
 z=9x+12y．
作出可行域（如图），
作出在一组平行直线9x+12y=t（t为参数），
此直线经过A（24，24），故z的最优解为（24，24），
z的最大值为9×24+12×24=504（万元），
故生产A、B两种产品各24吨时，才能获得最大的利润；最大的利润是504万元

点评 本题主要考查线性规划的应用，建立不等式关系，列出目标函数，利用数形结合是解决线性规划问题中的基本方法．