题目内容
1.若x,y∈R+,且x+y=1,则$\frac{1}{x}+\frac{1}{y}$的取值范围是( )| A. | (2,+∞) | B. | [2,+∞) | C. | (4,+∞) | D. | [4,+∞) |
分析 x+y=1代入$\frac{1}{x}+\frac{1}{y}$,然后根据基本不等式即可求出$\frac{1}{x}+\frac{1}{y}$的范围,从而找出正确选项.
解答 解:x,y>0,且x+y=1;
∴$\frac{1}{x}+\frac{1}{y}=\frac{x+y}{x}+\frac{x+y}{y}$
=$1+\frac{y}{x}+\frac{x}{y}+1$
=$2+\frac{y}{x}+\frac{x}{y}$
≥2+2;
当$\frac{y}{x}=\frac{x}{y}$,即x=y时取“=”;
∴$\frac{1}{x}+\frac{1}{y}$的取值范围为[4,+∞).
故选D.
点评 考查基本不等式的应用,并判断等号能否取到.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
6.若实数a,b,c满足1<b<a<2,0<c<$\frac{1}{8}$,则关于x的方程ax2+bx+c=0( )
| A. | 在区间(-1,0)内没有实数根 | |
| B. | 在区间(-1,0)内有一个实数根,在(-1,0)外有一个实数根 | |
| C. | 在区间(-1,0)内有两个相等的实数根 | |
| D. | 在区间(-1,0)内有两个不相等的实数根 |
9.若方程组$\left\{\begin{array}{l}ax+by=1\\{x^2}+{y^2}=50\end{array}\right.$至少有一解,且所有的解都是整数解,则有序实数对(a,b)的组数为( )
| A. | 60 | B. | 66 | C. | 72 | D. | 78 |
5.已知直线l过抛物线y2=2px(p>0)的焦点F(1,0),交抛物线于M,N两点.
(Ⅰ)写出抛物线的标准方程及准线方程;
(Ⅱ)O为坐标原点,直线MO、NO分别交准线于点P,Q,求|PQ|的最小值.
(Ⅰ)写出抛物线的标准方程及准线方程;
(Ⅱ)O为坐标原点,直线MO、NO分别交准线于点P,Q,求|PQ|的最小值.
8.已知随机变量ξ的分布列如图所示,则函数a=0.3,E(ξ)=1.
| ξ | 0 | 1 | 2 |
| P | 0.3 | 0.4 | a |
 满足对任意的实数
满足对任意的实数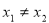 都有
都有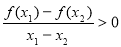 ,则a的取值范围是( )
,则a的取值范围是( )