题目内容
甲乙两人通过考试的概率分别为
和
,两人同时参加考试,其中恰有一人通过的概率是( )
| 3 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:记甲乙两人通过考试分别为事件A、B,则有P(A)=
,P(B)=
,所求的事件可表示为
B+A
,由事件的独立性和互斥性,即可求出其中恰有一人通过的概率是多少.
| 3 |
| 5 |
| 1 |
| 3 |
. |
| A |
. |
| B |
解答:
解:记甲、乙甲乙两人通过考试分别为事件A、B,
则有P(A)=
,P(B)=
,
所求的事件可表示为
B+A
,
P(
B+A
)=P(
)P(B)+P(A)P(
)
=(1-
)×
+
×(1-
)
=
×
+
×
=
故选:C.
则有P(A)=
| 3 |
| 5 |
| 1 |
| 3 |
所求的事件可表示为
. |
| A |
. |
| B |
P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
. |
=(1-
| 3 |
| 5 |
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 3 |
=
| 2 |
| 5 |
| 1 |
| 3 |
| 3 |
| 5 |
| 2 |
| 3 |
=
| 8 |
| 15 |
故选:C.
点评:本题主要考查了相互独立的事件发生的概率,包含事件的互斥性的应用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
由曲线y2=x与y=x,y=
所围成图形的面积是( )
| 3 |
A、S=
| ||||||
B、S=
| ||||||
C、S=
| ||||||
D、S=
|
已知f(x)=π(x∈R),则f(π2)=( )
| A、π2 | ||
| B、π | ||
C、
| ||
| D、不确定 |
若关于x的不等式x2-x+a>0恒成立,则a的取值范围为( )
A、[
| ||
B、(
| ||
C、(-∞,
| ||
D、(-∞,
|
若执行如图所示的程序框图,当输入n=1,m=5,则输出p的值为( )


| A、-4 | B、1 | C、2 | D、5 |
在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其它7个小长方形的面积和的
,且样本容量为200,则第8组的频数为( )
| 1 |
| 4 |
| A、40 | B、0.2 |
| C、50 | D、0.25 |
 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,
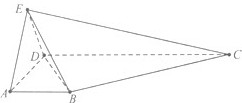 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=