题目内容
17.已知函数$f(x)=\sqrt{1+{x^2}}$,x∈R.(1)证明对?a、b∈R,且a≠b,总有:|f(a)-f(b)|<|a-b|;
(2)设a、b、c∈R,且$a+b+c=f(2\sqrt{2})$,证明:a+b+c≥ab+bc+ca.
分析 (1)利用放缩法和绝对值三角不等式的性质即可证明,
(2)由已知a+b+c=3,利用基本不等式即可证明
解答 证明:(1)$|f(a)-f(b)|=|\sqrt{1+{a^2}}-\sqrt{1+{b^2}}|=\frac{{|1+{a^2}-1-{b^2}|}}{{\sqrt{1+{a^2}}+\sqrt{1+{b^2}}}}$$<\frac{{|{a^2}-{b^2}|}}{{\sqrt{a^2}+\sqrt{b^2}}}=\frac{|a-b||a+b|}{|a|+|b|}≤\frac{|a-b||a+b|}{|a+b|}=|a-b|$
若a+b=0时,不等式显然成立.
(2)由已知a+b+c=3,
则3(a+b+c)=(a+b+c)2=a2+b2+c2+2ab+2bc+2ca,
=$\frac{1}{2}({a^2}+{b^2})+\frac{1}{2}({b^2}+{c^2})+\frac{1}{2}({c^2}+{a^2})+2ab+2bc+2ca$,
≥ab+bc+ca+2ab+2bc+2ca,
=3(ab+bc+ca)
故a+b+c≥ab+bc+ca.
点评 本题考查了绝对值的三角不等式和基本不等式的应用,考查了学生的转化能力,属于中档题

练习册系列答案
相关题目
1.某校举行高二理科学生的数学与物理竞赛,并从中抽取72名学生进行成绩分析,所得学生的及格情况统计如表:
(1)根据表中数据,判断是否是99%的把握认为“数学及格与物理及格有关”;
(2)若以抽取样本的频率为概率,现在该校高二理科学生中,从数学及格的学生中随机抽取3人,记X为这3人中物理不及格的人数,从数学不及格学生中随机抽取2人,记Y为这2人中物理不及格的人数,记ξ=|X-Y|,求ξ的分布列及数学期望.
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{21}{n}_{12})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
| 物理及格 | 物理不及格 | 合计 | |
| 数学及格 | 28 | 8 | 36 |
| 数学不及格 | 16 | 20 | 36 |
| 合计 | 44 | 28 | 72 |
(2)若以抽取样本的频率为概率,现在该校高二理科学生中,从数学及格的学生中随机抽取3人,记X为这3人中物理不及格的人数,从数学不及格学生中随机抽取2人,记Y为这2人中物理不及格的人数,记ξ=|X-Y|,求ξ的分布列及数学期望.
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{21}{n}_{12})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
| P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
8.某四棱锥的三视图如图所示,则最长的一条侧棱的长度是( )
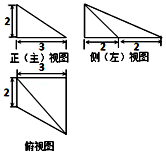

| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
9.执行如图所示的程序框图,若输出的结果为S=1320,则判断框内应填入的内容是( )


| A. | K<9? | B. | K<10? | C. | K<11? | D. | K<12? |
6.已知过曲线$\left\{\begin{array}{l}{x=3sinθ}\\{y=3cosθ}\end{array}\right.$(θ为参数,0≤θ≤π)上一点P与原点O的直线PO的倾斜角为$\frac{π}{2}$,则P点坐标是( )
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
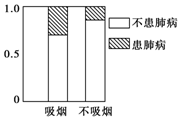 根据如图所示的等高条形图回答,吸烟与患肺病有关系.(“有”或“没有”)
根据如图所示的等高条形图回答,吸烟与患肺病有关系.(“有”或“没有”)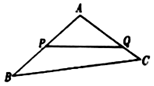 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.