题目内容
20.作出函数y=cosx|tanx|(0≤x<$\frac{3π}{2}$,且x≠$\frac{π}{2}$)的图象.分析 根据x的取值情况分类讨论,去掉|tanx|中的绝对值符号,转化为分段函数,利用正弦函数的图象即可得解.
解答 解:∵y=cosx|tanx|=$\left\{\begin{array}{l}{\stackrel{sinx}{-sinx}}&{\stackrel{0≤x<\frac{π}{2}}{\frac{π}{2}<x≤π}}\\{-sinx}&{π<x<\frac{3π}{2}}\end{array}\right.$,
∴函数y=cosx|tanx|(0≤x≤$\frac{3π}{2}$,且x≠$\frac{π}{2}$)的图象如下: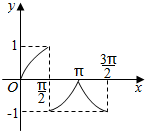 .
.
点评 本题考查正切函数与正弦函数的图象,确定绝对值符号是关键,考查分类讨论思想,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
11.在△ABC中,a=5,b=4,C=60°,则$\overrightarrow{CB}$•$\overrightarrow{CA}$的值为( )
| A. | -10 | B. | 10 | C. | -10$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
15.函数f(x)=ax2-2x+3在(-∞,1]上是减函数,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (0,1] | C. | [1,+∞) | D. | [0,1] |
12.设x,y∈R,则“x,y≥1”是“x2+y2≥2”的( )
| A. | 既不充分也不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
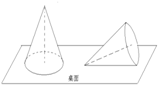 用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.