题目内容
设集合A={x|x2-3x+2=0},B={x|ax+1=0}.
(1)若A∩B={2},求实数a的值;
(2)若B⊆A,求实数a的值.
(1)若A∩B={2},求实数a的值;
(2)若B⊆A,求实数a的值.
考点:交集及其运算,集合的包含关系判断及应用
专题:集合
分析:(1)由A∩B={2}得2∈B,把2代入ax+1=0代入求出a的值;
(2)由x2-3x+2=0求出集合A,由子集的定义和B⊆A求出B所有的情况,再依次代入求出a的值.
(2)由x2-3x+2=0求出集合A,由子集的定义和B⊆A求出B所有的情况,再依次代入求出a的值.
解答:
解:(1)因为A∩B={2},所以2∈B,
则2a+1=0,解得a=-
,
(2)由x2-3x+2=0得,x=1或x=2,则A={1,2},
因为B⊆A,所以B=∅或{1}或{2},
当B=∅时,则a=0,
当B={1}时,则a+1=0,得a=-1,
当B={2}时,则2a+1=0,得a=-
,
综上得,实数a的值是0或-1或-
.
则2a+1=0,解得a=-
| 1 |
| 2 |
(2)由x2-3x+2=0得,x=1或x=2,则A={1,2},
因为B⊆A,所以B=∅或{1}或{2},
当B=∅时,则a=0,
当B={1}时,则a+1=0,得a=-1,
当B={2}时,则2a+1=0,得a=-
| 1 |
| 2 |
综上得,实数a的值是0或-1或-
| 1 |
| 2 |
点评:本题考查交集及其运算,子集的定义,以及一元二次方程的解法,属于基础题.

练习册系列答案
相关题目
已知a=20.5,b=lg2,c=ln2,则( )
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、a>c>b |
已知sin2α=
,则cos(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知一个算法,如图所示,则输出的结果是( )


| A、10 | B、11 | C、8 | D、9 |
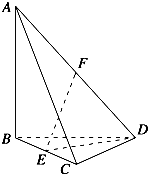 如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点.
如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点.