题目内容
设动点P(x,y)在区域Q:
上,过点P任作直线l,设直线l与区域Q的公共部分为线段AB,则以AB
为直径的圆的面积的最大值为( )
|
为直径的圆的面积的最大值为( )
| A、π | B、2π | C、3π | D、4π |
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,利用数形结合得到圆的最大直径,则圆的最大面积可求.
解答:
 解:作出不等式组表示的平面区域,
解:作出不等式组表示的平面区域,
得到如图的△MNO及其内部,
其中M(0,4),N(2,2),0为坐标原点
∵直线l与区域Ω的公共部分为线段AB,
∴当直线l与y轴重合时,|AB|=|OM|=4达到最大值,
此时圆的半径为2,
此时以AB为直径的圆的面积为S=π•22=4π,
故选:D
 解:作出不等式组表示的平面区域,
解:作出不等式组表示的平面区域,得到如图的△MNO及其内部,
其中M(0,4),N(2,2),0为坐标原点
∵直线l与区域Ω的公共部分为线段AB,
∴当直线l与y轴重合时,|AB|=|OM|=4达到最大值,
此时圆的半径为2,
此时以AB为直径的圆的面积为S=π•22=4π,
故选:D
点评:本题主要考查线性规划的应用,根据条件利用数形结合是解决本题的关键.

练习册系列答案
相关题目
下列命题正确的是( )
| A、?x∈R,都有x2-3x+3>0成立 |
| B、?x0∈R,使sin2x0+cos2x0<1成立 |
| C、“?x0∈R,使x02-1<0”的否定是“?x∈R,都有x2-1>0” |
| D、若“p∨q”为假,则命题p、q中一个真另一个假 |
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3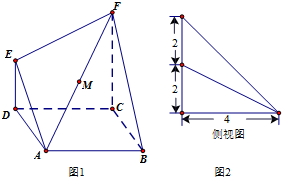 在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=
在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=