题目内容
函数y=x（sin2x-cos2x）的图象关于 对称．
考点：二倍角的余弦
专题：函数的性质及应用
分析：令f（x）=x（sin2x-cos2x）=-xcos2x，利用奇偶函数的概念可判定y=f（x）为奇函数，从而可得答案．
解答：
解：∵y=f（x）=x（sin2x-cos2x）=-xcos2x，
∴f（-x）=-（-x）cos（-2x）=xcos2x=-（-xcos2x）=-f（x），
∴函数y=x（sin2x-cos2x）为奇函数，
∴其图象关于原点（0，0）对称，
故答案为：（0，0）．
∴f（-x）=-（-x）cos（-2x）=xcos2x=-（-xcos2x）=-f（x），
∴函数y=x（sin2x-cos2x）为奇函数，
∴其图象关于原点（0，0）对称，
故答案为：（0，0）．
点评：本题考查二倍角的余弦，着重考查函数奇偶性的概念及应用，属于中档题．
练习册系列答案
相关题目
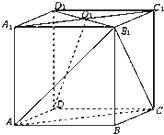已知正方体ABCD-A1B1C1D1中，面A1B1C1D1中心为O1．
如图给出的是计算