题目内容
已知函数f(x)=3cos2
+sin2
-2,则f′(
)= .
| x |
| 2 |
| x |
| 2 |
| 2π |
| 3 |
考点:导数的运算
专题:函数的性质及应用,导数的综合应用
分析:先对函数化简,然后求导数,代入求值即可.
解答:
解:∵f(x)=3cos2
+sin2
-2=2cos2
-1=cosx,
∴f′(x)=-sinx,
则f′(
)=-sin
=-sin(π-
)=-sin
=-
.
故答案为:-
.
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴f′(x)=-sinx,
则f′(
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:本题考查三角函数的化简,需要熟练使用相应的公式,还考察了三角函数求导,属于基础题目,需熟练掌握公式.

练习册系列答案
相关题目
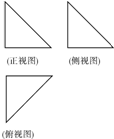 已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )
已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )A、6+2
| ||
B、6+4
| ||
C、12+4
| ||
D、8+4
|
已知集合A={x|mx2-mx+1=0}只有一个真子集,则实数m的值为( )
| A、0 | B、4 | C、0或4 | D、0或-4 |
设a=
,b=tan10°+tan50°+
tan10°•tan50°,则下列各式正确的为( )
| 1+tan10° |
| 1-tan10° |
| 3 |
A、a<b<
| ||
B、a<
| ||
C、b<
| ||
D、b<a<
|
函数f(x)=x|x|-x3是 ( )
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |