题目内容
已知焦点为F,准线为l的抛物线Γ:x2=2py(p>0)经过点(-2
,3),其中A,B是抛物线上两个动点,O为坐标原点.
(1)求抛物线Γ的方程.
(2)若OA⊥OB,求线段AB的中点P的轨迹方程.
(3)若∠AFB=90°,线段AB的中点M,点M在直线l上的投影为N,求
的最大值.
| 3 |
(1)求抛物线Γ的方程.
(2)若OA⊥OB,求线段AB的中点P的轨迹方程.
(3)若∠AFB=90°,线段AB的中点M,点M在直线l上的投影为N,求
| |MN| |
| |AB| |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用抛物线Γ:x2=2py(p>0)经过点(-2
,3),求出p,即可求抛物线Γ的方程.
(2)若OA⊥OB,则x1x2+y1y2=0,利用2x=x2+x1,2y=
+
,即可求线段AB的中点P的轨迹方程.
(3)设|AF|=a、|BF|=b,由抛物线定义结合梯形的中位线定理,得2|MN|=a+b.再由勾股定理得|AB|2=a2+b2,结合基本不等式求得|AB|的范围,从而可得
的最大值.
| 3 |
(2)若OA⊥OB,则x1x2+y1y2=0,利用2x=x2+x1,2y=
| x12 |
| 4 |
| x22 |
| 4 |
(3)设|AF|=a、|BF|=b,由抛物线定义结合梯形的中位线定理,得2|MN|=a+b.再由勾股定理得|AB|2=a2+b2,结合基本不等式求得|AB|的范围,从而可得
| |MN| |
| |AB| |
解答:
解:(1)∵抛物线Γ:x2=2py(p>0)经过点(-2
,3),
∴12=6p,∴p=2,
∴抛物线Γ的方程为x2=4y.
(2)设P(x,y),A(x1,
),B(x2,
),则
2x=x2+x1,2y=
+
∴x2x1=2x2-4y,
∵OA⊥OB,
∴x1x2+y1y2=0,
∴x1x2+
•
=0,
∴x2x1=-16,
∴2x2-4y=-16,
即y=
x2+4,
∴线段AB的中点P的轨迹方程是y=
x2+4;
(3)设|AF|=a,|BF|=b,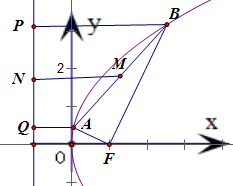 A、B在准线上的射影点分别为Q、P,连接AQ、BP
A、B在准线上的射影点分别为Q、P,连接AQ、BP
由抛物线定义,得AF|=|AQ|且|BF|=|BP|
在梯形ABPQ中根据中位线定理,得2|MN|=|AQ|+|BP|=a+b.
由勾股定理得|AB|2=a2+b2,配方得|AB|2=(a+b)2-2ab,
又∵ab≤(
) 2,
∴(a+b)2-2ab≥(a+b)2-2×(
) 2=
(a+b)2
得到|AB|≥
(a+b).
∴
≤
=
,即
的最大值为
.
| 3 |
∴12=6p,∴p=2,
∴抛物线Γ的方程为x2=4y.
(2)设P(x,y),A(x1,
| x12 |
| 4 |
| x22 |
| 4 |
2x=x2+x1,2y=
| x12 |
| 4 |
| x22 |
| 4 |
∴x2x1=2x2-4y,
∵OA⊥OB,
∴x1x2+y1y2=0,
∴x1x2+
| x12 |
| 4 |
| x22 |
| 4 |
∴x2x1=-16,
∴2x2-4y=-16,
即y=
| 1 |
| 2 |
∴线段AB的中点P的轨迹方程是y=
| 1 |
| 2 |
(3)设|AF|=a,|BF|=b,
 A、B在准线上的射影点分别为Q、P,连接AQ、BP
A、B在准线上的射影点分别为Q、P,连接AQ、BP 由抛物线定义,得AF|=|AQ|且|BF|=|BP|
在梯形ABPQ中根据中位线定理,得2|MN|=|AQ|+|BP|=a+b.
由勾股定理得|AB|2=a2+b2,配方得|AB|2=(a+b)2-2ab,
又∵ab≤(
| a+b |
| 2 |
∴(a+b)2-2ab≥(a+b)2-2×(
| a+b |
| 2 |
| 1 |
| 2 |
得到|AB|≥
| ||
| 2 |
∴
| |MN| |
| |AB| |
| ||||
|
| ||
| 2 |
| |MN| |
| |AB| |
| ||
| 2 |
点评:本题着重考查抛物线的方程、考查了抛物线的定义与简单几何性质、梯形的中位线定理和基本不等式求最值等知识,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
集合M={x|x=1+a2,a∈N*},P={y|y=x2-4x+5,x∈N*},下列关系中正确的是( )
| A、M?P | B、P?M |
| C、M=P | D、M?P且P?M |
 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则