题目内容
集合M={x|x=1+a2，a∈N*}，P={y|y=x2-4x+5，x∈N*}，下列关系中正确的是（ ）
| A、M?P | B、P?M |
| C、M=P | D、M?P且P?M |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：由题意，可先化简P集合，对基本的表达式进行配方，再根据两集合中元素的结构判断出两集合的包含关系
解答：
解：P={y|y=x2-4x+5，x∈N*}={y|y=（x-2）2+1，x∈N*}，可知，P集合中的元素是全体自然数的平方加1，
又M={x|x=1+a2，a∈N*}，其中的元素是全体正整数的平方加1，
所以M?P
故选：A
又M={x|x=1+a2，a∈N*}，其中的元素是全体正整数的平方加1，
所以M?P
故选：A
点评：本题考查两集合间包含关系，对集合中元素的形式进行化简是解答的关键
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
设f（x）可导，且y=f（e2x），则y′=（ ）
| A、f′（e2x） |
| B、f′（e2x）e2x |
| C、2f′（e2x） |
| D、2f′（e2x）e2x |
设y=ln（2x+3），则y′=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
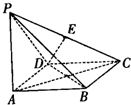四棱锥P-ABCD的底面为棱形，且∠DAB=60°，PA⊥底面ABCD，AB=2a，PA=2
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人，吴老师采用A、B两种不同的教学方式分别在甲、乙两个班进行教学实验．为了解教学效果，期末考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图所示．记成绩不低于90分者为“成绩优秀”．