题目内容
1.已知函数f(x)对任意x∈R都有f(x+6)+f(x)=2f(3),y=f(x-1)的图象关于点(1,0)对称,且f(4)=4,则f(2012)=( )| A. | 0 | B. | -4 | C. | -8 | D. | -16 |
分析 先利用函数y=f(x-1)的图象关于点(1,0)对称,得到函数y=f(x)是奇函数,然后求出f(3)=0,最后利用函数的周期性求f(2012)的值.
解答 解:因为函数y=f(x-1)的图象关于点(1,0)对称,
所以函数y=f(x)的图象关于点(0,0)对称,
即函数y=f(x)是奇函数,
令x=-3得,f(-3+6)+f(-3)=2f(3),
即f(3)-f(3)=2f(3),解得f(3)=0.
所以f(x+6)+f(x)=2f(3)=0,即f(x+6)=-f(x),
所以f(x+12)=f(x),即函数的周期是12.
所以f(2012)=f(12×168-4)=f(-4)=-f(4)=-4.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
12.已知过抛物线y2=4x焦点F的直线l交抛物线于A、B两点(点A在第一象限),若$\overrightarrow{AF}$=3$\overrightarrow{FB}$,则直线l的方程为( )
| A. | x-2y-1=0 | B. | 2x-y-2=0 | C. | x-$\sqrt{3}$y-1=0 | D. | $\sqrt{3}$x-y-$\sqrt{3}$=0 |
9.设集合S={x|x2-5x+6≥0},T={x|x>1},则S∩T=( )
| A. | [2,3] | B. | (1,2]∪[3,+∞) | C. | [3,+∞) | D. | (0,2]∪[3,+∞) |
16.已知函数y=f(x=2)是偶函数,且当x≠2时其导函数f′(x)满足(x-2)f′(x)>0,若2<a<3,则下列不等式式成立的是( )
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |
6.已知直线l的方向向量为$\vec s=(1,2,x)$,平面α的法向量$\vec n=(-2,y,2)$,若l?α,则xy的最大值为( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
13.阅读如图的程序框图,则输出的S等于( )
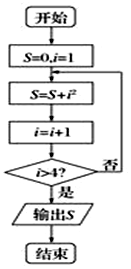

| A. | 55 | B. | 30 | C. | 20 | D. | 10 |
10.近年来我国电子商务行业迎来发展的新机遇.2016年双11期间,某购物平台的销售业绩高达918亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都作出好评的交易为80次.
(1)能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视作概率,某人在该购物平台上进行5次购物中,设对商品和服务全好评的次数为随机变量X:
①求对商品和服务全为好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方程.
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(1)能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视作概率,某人在该购物平台上进行5次购物中,设对商品和服务全好评的次数为随机变量X:
①求对商品和服务全为好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方程.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |