题目内容
6.等差数列{an}的首项a1=$\frac{1}{2}$,前三项和为$\frac{9}{2}$,点Pn(an,bn)(n∈N*)在函数y=log32x的图象上.(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若cn=3bn+2n,求数列{cn}的前n项和Sn.
分析 (Ⅰ)求出等差数列的首项与通项公式,即可求解数列{an}的通项公式,利用Pn(an,bn)(n∈N*)在函数y=log32x的图象上即可求解{bn}的通项公式;
(Ⅱ)化简cn=3bn+2n,利用等差数列以及等比数列求和公式求解数列{cn}的前n项和Sn.
解答 解:( I)等差数列{an}的首项a1=$\frac{1}{2}$,前三项和为$\frac{9}{2}$,a2=$\frac{3}{2}$,
等差数列{an}的首项a1=$\frac{1}{2}$,公差d=1,故an=n-$\frac{1}{2}$,
即数列{an}的通项公式为:an=n-$\frac{1}{2}$;
点Pn(an,bn)在函数y=log32x的图象上,则bn=log32an=log3(2n-1),
即数列{bn}的通项公式为bn=log3(2n-1),.
( II)cn=3bn+2n=2n-1+2n,
Sn=(1+3+5+…+(2n-1))+(21+22+…+2n)=$\frac{n(1+2n-1)}{2}$+$\frac{2(1-{2}^{n})}{1-2}$=n2+2n+1-2,
数列{cn}的前n项和Sn=n2+2n+1-2.
点评 本题考查数列与函数的综合应用,等差数列以及等比数列的通项公式以及数列求和的基本方法的应用,考查计算能力.

练习册系列答案
相关题目
17.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是( )
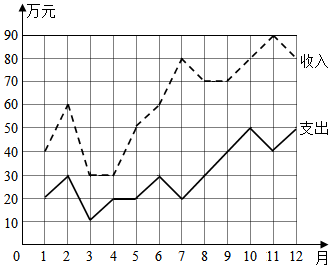
(注:结余=收入-支出)

(注:结余=收入-支出)
| A. | 收入最高值与收入最低值的比是3:1 | |
| B. | 结余最高的月份是7月 | |
| C. | 1至2月份的收入的变化率与4至5月份的收入的变化率相同 | |
| D. | 前6个月的平均收入为40万元 |
16.A、B、C、D、E五位抗战老兵应邀参加了在北京举行的“纪念抗战胜利70周年”大阅兵的老兵方队,现安排这五位老兵分别坐在某辆检阅车的前五排(每两人均不坐同一排),则事件“C坐中间一排,但A与B均不坐第一排”的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{4}$ |
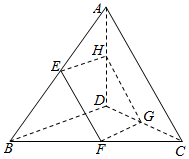 如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,DA的中点,且AC=BC.求证:四边形EFGH是菱形.
如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,DA的中点,且AC=BC.求证:四边形EFGH是菱形.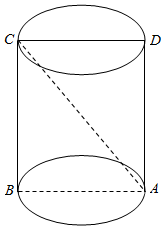 如图所示,已知圆柱的轴截面是一个正方形ABCD,圆柱的全面积为6πcm2,求
如图所示,已知圆柱的轴截面是一个正方形ABCD,圆柱的全面积为6πcm2,求