题目内容
已知一个几何体的三视图如图所示，根据图中尺寸可得该几何体的表面积为（ ）
A、12+4
| ||
| B、16 | ||
C、14+2
| ||
| D、20 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何是一个以俯视图为底面的棱柱，分别求出底面面积，底面周长和棱柱的高，进而可得几何体的表面积．
解答：
解：由已知中的三视图可得，该几何是一个以俯视图为底面的棱柱，
∵底面是一个直角边长为2的等腰直角三角形，
故底面面积S底=
×2×2=2，
底面周长C=2+2+
=4+2
，
又∵棱柱的高h=2．
故该几何体的表面积S=2×S底+Ch=2×2+（4+2
）×2=12+4
，
故选：A．
∵底面是一个直角边长为2的等腰直角三角形，
故底面面积S底=
| 1 |
| 2 |
底面周长C=2+2+
| 22+22 |
| 2 |
又∵棱柱的高h=2．
故该几何体的表面积S=2×S底+Ch=2×2+（4+2
| 2 |
| 2 |
故选：A．
点评：本题考查的知识点是由三视图求表面积，其中分析出几何体的形状是解答的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数y=sin（2x-
）的一条对称轴为（ ）
| π |
| 6 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=-
|
设f（x）是定义在R上的偶函数，且在（-∞，0）上是增函数，设a=f（log47），b=f（log
3），c=f（2
），则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| 2 |
| A、c＜a＜b |
| B、c＜b＜a |
| C、b＜c＜a |
| D、a＜b＜c |
设已知a，b，m均为整数（m＞0），若a和b被m除所得的余数相同，则称a和b对模m同余，记为a≡b（modm），若a=C
+C
•2+C
•22+…+C
•240，且a≡b（mod10），则b的值可以是（ ）
0 40 |
1 40 |
3 40 |
40 40 |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
在数列{an}中，若a1=-2，且对任意的n∈N*有2an+1=1+2an，则数列{an}前10项的和为（ ）
| A、5 | ||
| B、10 | ||
C、
| ||
D、
|
已知数列{an}满足：am=
（am-1+am+1）（m＞1，m∈N），a4=4，则a3+a4+a5=（ ）
| 1 |
| 2 |
| A、4 | B、8 | C、12 | D、16 |
在△ABC中，若a、b、c分别为角A、B、C所对的边，且cos2B+cosB+cos（A-C）=1，则有（ ）
| A、a、c、b 成等比数列 |
| B、a、c、b 成等差数列 |
| C、a、b、c 成等差数列 |
| D、a、b、c成等比数列 |
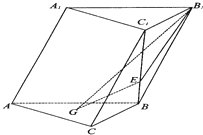如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，AA1=2．底面ABC是边长为2的正三角形，其重心为G点，E是线段BC1上一点，且BE=