题目内容
11.设不等式|x-4|-|2x-7|>$\frac{1}{3}$(x-7)的解集为M.(1)求M;
(2)证明:当a、b∈M时,|$\sqrt{ab}$-2|<|2$\sqrt{a}$-$\sqrt{b}$|.
分析 (1)分类讨论解不等式,可得M;
(2)利用反证法,即可证明.
解答 (1)解:x<3.5时,不等式化为4-x+2x-7>$\frac{1}{3}$(x-7),解得x>1,∴1<x<3.5;
3.5≤x<4时,不等式化为4-x-2x+7>$\frac{1}{3}$(x-7),解得x<4,∴3.5≤x<4;
x≥4时,不等式化为x-4-2x+7>$\frac{1}{3}$(x-7),解得x<4,无解;
综上所述,M={x|1<x<4};
(2)证明:要证明|$\sqrt{ab}$-2|<|2$\sqrt{a}$-$\sqrt{b}$|,
只要证明ab-4$\sqrt{ab}$+4<4a-4$\sqrt{ab}$+b,
只要证明ab+4<4a+b,
只要证明ab+4<4a+b,
只要证明(a-1)(b-4)<0,
∵a、b∈M={x|1<x<4},∴结论成立.
点评 本题考查不等式的解法与证明,考查分析法的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
1.Sn是数列{an}的前n项和,Sn=3an-2a1,a3=$\frac{1}{4}$,bn=anlnan,则数列{bn}的最小项是( )
| A. | 第3项 | B. | 第4项 | C. | 第5项 | D. | 第6项 |
2.已知直线x+y=m(m>0)与圆x2+y2=1相交于P,Q两点,且∠POQ=120°(其中O为原点),那么m的值是( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
19.甘肃省瓜州县自古就以生产“美瓜”面名扬中外,生产的“瓜州蜜瓜”有4个系列30多个品种,质脆汁多,香甜可口,清爽宜人,含糖量达14%~19%,是消暑止渴的佳品,调查表明,蜜瓜的甜度与海拔高度,日照时长,温差有极强的相关性,分别用x,y,z表示蜜瓜甜度与海拔高度,日照时长,温差的相关程度,big对它们进行量化:0表示一般,1表示良,2表示优,在用综合指标w=x+y+z的值平定蜜瓜的顶级,若w≥4,则为一级;若2≤w≤3,则为二级;若0≤w≤1,则为三级,今年来,周边各省也开始发展蜜瓜种植,为了了解目前蜜瓜在周边各省的种植情况,研究人员从不同省份随机抽取了10块蜜瓜种植地,得到如下结果:
(1)若有蜜瓜种植地110块,试估计等级为三家的蜜瓜种植地的数量;
(2)从样本里等级为一级的蜜瓜种植地中随机抽取两块,求这两块种植地的综合指标w至少有一个为4的概率.
| 种植地编号 | A | B | C | D | E |
| (x,y,z) | (1,0,0) | (2,2,1) | (0,1,1) | (2,0,2) | (1,1,1) |
| 种植地编号 | F | G | H | I | J |
| (x,y,z) | (1,1,2) | (2,2,2) | (0,0,1) | (2,2,1) | (0,2,1) |
(2)从样本里等级为一级的蜜瓜种植地中随机抽取两块,求这两块种植地的综合指标w至少有一个为4的概率.
3.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-2y+4≥0}\\{2x-y-4≤0}\end{array}\right.$,若x2+y2+2x≥k恒成立,则实数k的最大值为( )
| A. | 40 | B. | 9 | C. | 8 | D. | $\frac{7}{2}$ |
8.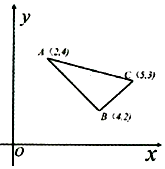 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | -1<a<1 | B. | -1≤a≤1 | C. | -1≤a<1 | D. | -1<a≤1 |