题目内容
1.Sn是数列{an}的前n项和,Sn=3an-2a1,a3=$\frac{1}{4}$,bn=anlnan,则数列{bn}的最小项是( )| A. | 第3项 | B. | 第4项 | C. | 第5项 | D. | 第6项 |
分析 运用数列的递推式,结合等比数列的定义和通项公式,可得an,再由函数y=xlnx,求得导数和单调区间和最小值点,考虑数列{an}中与最值点的距离,找出较小的即可.
解答 解:∵Sn=3an-2a1,∴n=1时,a1=3a1-2a1,
n≥2时,an=Sn-Sn-1=3an-2a1-(3an-1-2a1),化为:an=$\frac{3}{2}$an-1.
∵a3=$\frac{1}{4}$,
∴a2=$\frac{2}{3}$×$\frac{1}{4}$=$\frac{1}{6}$,a1=$\frac{2}{3}$×$\frac{1}{6}$=$\frac{1}{9}$,
∴an=$\frac{1}{9}$×($\frac{3}{2}$)n-1,
由函数y=xlnx的导数为y′=1+lnx,
可得x>$\frac{1}{e}$时,y′>0,函数y递增;
0<x<$\frac{1}{e}$时,y′<0,函数y递减.
即有函数y在x=$\frac{1}{e}$处取得极小值,且为最小值.
而数列{an}递增,且a3=$\frac{1}{4}$;a4=$\frac{3}{8}$,
由|a3-$\frac{1}{e}$|>|a4-$\frac{1}{e}$|,
故数列{bn}的最小项是第四项.
故选:B.
点评 本题考查了数列最小项的求法,考查数列的递推式和等比数列的通项公式的运用,考查转化思想的运用,考查了计算能力,属于中档题.

练习册系列答案
相关题目
11.下列函数中,既是偶函数又是(0,+∞)上的增函数的是( )
| A. | y=x3 | B. | y=2|x| | C. | y=-x2 | D. | y=log3(-x) |
9.(1-$\sqrt{x}$)6(1-$\root{3}{x}$)4的展开式中,x2的系数是( )
| A. | -75 | B. | -45 | C. | 45 | D. | 75 |
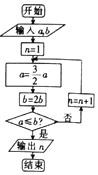 名著《算学启蒙》中有如下题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”.这段话的意思是:“松有五尺长,竹有两尺长,松每天增长前一天长度的一半,竹每天增长前一天长度的两倍.”.为了研究这个问题,以a代表松长,以b代表竹长,设计了如图所示的程序框图,输入的a,b的值分别为5,2,则输出的n的值为( )
名著《算学启蒙》中有如下题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”.这段话的意思是:“松有五尺长,竹有两尺长,松每天增长前一天长度的一半,竹每天增长前一天长度的两倍.”.为了研究这个问题,以a代表松长,以b代表竹长,设计了如图所示的程序框图,输入的a,b的值分别为5,2,则输出的n的值为( )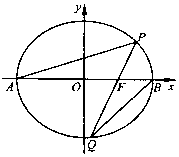 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).