题目内容
已知点A（1，2），F（2，0），点P为椭圆
+
=1上一点，则|PA|+2|PF|的最小值为： ．
| x2 |
| 16 |
| y2 |
| 12 |
考点：椭圆的简单性质
专题：圆锥曲线中的最值与范围问题
分析：过P作PB⊥l，交l与B，由椭圆的第二定义知|PB|=2|PF|，由两点间线段最短知当A，P，B三点共线时，|PA|+2|PF|的最小值，由此能求出结果．
解答：
解：如图，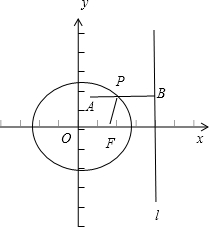
椭圆
+
=1中，
∵a=4，b=2
，c=2，e=
=
，
∴点A（1，2）椭圆内，F（2，0）是椭圆的右焦点，
椭圆的右准l：x=
=8，
过P作PB⊥l，交l与B，
由椭圆的第二定义知：
=
，
∴|PB|=2|PF|，
∴|PA|+2|PF|=|PA|+|PB|，
由两点间线段最短知当A，P，B三点共线时，
|PA|+2|PF|的最小值，其最小值=8-1=7．
故答案为：7．
椭圆| x2 |
| 16 |
| y2 |
| 12 |
∵a=4，b=2
| 3 |
| c |
| a |
| 1 |
| 2 |
∴点A（1，2）椭圆内，F（2，0）是椭圆的右焦点，
椭圆的右准l：x=
| 16 |
| 2 |
过P作PB⊥l，交l与B，
由椭圆的第二定义知：
| |PF| |
| |PB| |
| 1 |
| 2 |
∴|PB|=2|PF|，
∴|PA|+2|PF|=|PA|+|PB|，
由两点间线段最短知当A，P，B三点共线时，
|PA|+2|PF|的最小值，其最小值=8-1=7．
故答案为：7．
点评：本题考查与椭圆有关的两条线段和的最小值的求法，是中档题，解题时要熟练掌握椭圆的定义，注意数形结合思想的合理运用．
练习册系列答案
通城学典默写能手系列答案
相关题目
已知直线L经过点A（1，2
），B（2，
），则L的倾斜角是（ ）
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
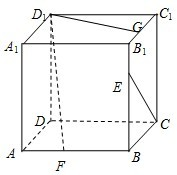已知正方体ABCD-A1B1C1D1，点E、F、G分别是棱B1B、AB和B1C1上的动点，观察直线CE与D1F，CE与D1G．已知三点A（a，2），B（5，1），C（-4，2a）在同一直线上，则a的值是（ ）
| A、1或2 | ||
B、2或
| ||
C、2或-
| ||
| D、1或-2 |