题目内容
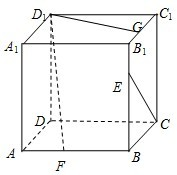 已知正方体ABCD-A1B1C1D1,点E、F、G分别是棱B1B、AB和B1C1上的动点,观察直线CE与D1F,CE与D1G.
已知正方体ABCD-A1B1C1D1,点E、F、G分别是棱B1B、AB和B1C1上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
①对于任意点E,存在点F,使得D1F⊥CE;
②对于任意点F,存在点E,使得CE⊥D1F;
③对于任意点E,存在点G,使得D1G⊥CE;
④对于任意点G,存在点E,使得CE⊥D1G.
其中,所有正确结论的序号是
考点:命题的真假判断与应用,直线与平面垂直的判定
专题:空间位置关系与距离
分析:建立空间直角坐标系,设出相关点的坐标,得出相关向量的坐标,利用两向量垂直的等价条件对应坐标乘积之和为0.
解答:
解:以D为坐标原点,以DC所在直线为x轴,以DA为直线为y轴,以DD1所在直线为z轴,建立空间直角坐标系.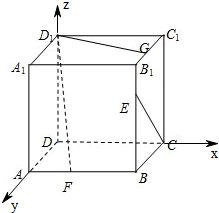
设正方体的边长为1,则C(1,0,0),D1(0,0,1),
设E(1,1,m),F(n,1,0),G(1,k,1),
则向量
=(0,1,m),
=(n,1,-1),
=(1,k,0),
所以
⊥
?0×n+1×1+m×(-1)=0?m=1;
⊥
?0×1+1×k+m×0=0?k=0,所以②③正确.
故答案为:②③.

设正方体的边长为1,则C(1,0,0),D1(0,0,1),
设E(1,1,m),F(n,1,0),G(1,k,1),
则向量
| CE |
| D1F |
| D1G |
所以
| CE |
| D1F |
| CE |
| D1G |
故答案为:②③.
点评:本题主要考查空间直线的位置关系:垂直,应用空间直角坐标系坐标之间的关系,是快速解题的关键,同学应掌握,本题是一道中档题.

练习册系列答案
相关题目
已知A={x|f(x)=lg(x2-x-2),x∈R},B={x||x-i|<
,i为虚数单位,x>0},则A∩B=( )
| 10 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知f(x)为偶函数,且f(2+x)=f(2-x),当-2≤x≤0时,f(x)=2x;若n∈N*,an=f(n),则a2013=( )
| A、2009 | ||
| B、-2009 | ||
C、
| ||
D、
|